题目内容
10.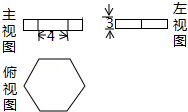 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | 72$\sqrt{3}$ | D. | 144$\sqrt{3}$ |
分析 首先确定该几何体的三视图,然后根据其尺寸确定其体积即可.
解答 解:观察三视图发现该几何体为底面边长为4,高为3的正六棱柱,
弦心距为$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
底面积为$\frac{1}{2}$×4×6×2$\sqrt{3}$=24$\sqrt{3}$,
其体积为:24$\sqrt{3}$×3=72$\sqrt{3}$,
故选C.
点评 本题考查了圆锥的计算,解题的关键是了解正六棱柱的体积的计算方法,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.关于反比例函数y=$\frac{2}{x}$的图象,下列说法正确的是( )
| A. | 图象经过点(1,1) | |
| B. | 当x<0时,y随x的增大而减小 | |
| C. | 图象的两个分支关于x轴成轴对称 | |
| D. | 图象的两个分支分布在第二、四象限 |
15.某学生为了描点作出函数y=ax2+bx+c(a≠0)的图象,取了自变量的7个值,x1<x2<…<x7且x2-x1=x3-x2=…=x7-x6,分别算出对应的y的值,列出如表;
但由于粗心算出了其中一个y的值,请指出算错的是哪一个值?正确的值是多少?并说明理由.
| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| y | 51 | 107 | 185 | 285 | 407 | 549 | 717 |
20. 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
 如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )
如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1、B2、B3、…都在直线y=x上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=2,则点B2011的坐标是( )| A. | (22010,22010) | B. | (22011,22011) | C. | (22010,22011) | D. | (22011,22012) |
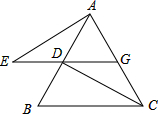 已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.
已知如图,△ABC是等边三角形,过AB边上的点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使DE=CG,连接AE、CD.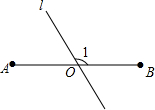 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.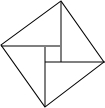 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( )
如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( ) 如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4.
如图,A点为反比例函数$y=\frac{k}{x}$图象上一点,过A点作AB⊥y轴,B为垂足,点P为x轴上任意一点,且△ABP的面积为2,则k=-4.