题目内容
20.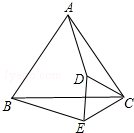 如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.
如图所示,已知:△ABC和△CDE都是等边三角形.求证:AD=BE.
分析 根据等边三角形的性质得到∠ACB=∠DCE=60°,于是得到∠ACD=∠BCE,即可证明△ACD≌△BCE,根据全等三角形对应边相等的性质即可解题.
解答 证明:∵△ABC和△CDE都是等边三角形,
∴∠ACB=∠DCE=60°,
∴∠ACD+∠BCD=∠ACB,∠BCE+∠BCD=∠DCE,
即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BCE是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
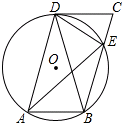 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE. 如图,△ABC和△AED为等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE.连接BE、CD交于点O,连接AO并延长交CE为点H.
如图,△ABC和△AED为等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE.连接BE、CD交于点O,连接AO并延长交CE为点H.