题目内容
2.已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+4|+|b-1|=0,A,B之间的距离记作|AB|,定义|AB|=|a-b|.(1)求线段AB的长|AB|;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值.
分析 (1)利用绝对值的非负性质得到a+4=0,b-1=0,解得a=-4,b=1,再根据题中定义得到|AB|=|-4-1|,然后根据绝对值的意义计算即可;
(2)根据数轴上两点之间的距离得定义得到|x+4|-|x-1|=2,然后分类原讨论:当x≤-4时,-x-4+x-1=2;当-4<x≤1时,x+4+x-1=2;当x>1时,x+4-x+1=2,再分别解方程求x即可.
解答 解:(1)∵|a+4|+|b-1|=0,
∴a+4=0,b-1=0,
∴a=-4,b=1,
∴|AB|=|-4-1|=5;
(2)根据题意得|x+4|-|x-1|=2,
当x≤-4时,-x-4+x-1=2,无解;
当-4<x≤1时,x+4+x-1=2,解得x=-0.5,
当x>1时,x+4-x+1=2,无解,
所以x的值为-0.5.
点评 本题考查了绝对值:当a是正数时,a的绝对值是它本身a; 当a是负数时,a的绝对值是它的相反数-a; 当a是零时,a的绝对值是零.

练习册系列答案
相关题目
13.钟面角是指时钟的时针与分针所成的角.从上午8点整到上午11点整,钟面角为90°的情况出现了( )
| A. | 6次 | B. | 5次 | C. | 4次 | D. | 3次 |
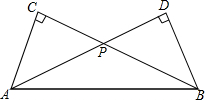 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=8,点P是BC边上的一个动点(不与B,C重合),过点B作射线AP的垂线,D为垂足,设CP=t.
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=8,点P是BC边上的一个动点(不与B,C重合),过点B作射线AP的垂线,D为垂足,设CP=t.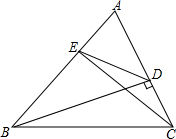 如图,△ABC中,BD⊥AC,CE⊥AB,AD•AE=$\frac{1}{4}$AB•AC,求cosA的值.
如图,△ABC中,BD⊥AC,CE⊥AB,AD•AE=$\frac{1}{4}$AB•AC,求cosA的值. 已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:∠B=∠C.
已知:如图,直线AD与BC交于点O,OA=OD,OB=OC.求证:∠B=∠C.