题目内容
14.代数式x2-xy+y2+x+y能分解为两个一次因式之积吗?若能,则分解因式;若不能,则证明此结论.分析 运用反证法,假设结论成立,即为(ax+by+e)(cx+dy+f),展开式子对比探讨得出答案即可.
解答 证明:运用反证法,假设结论成立,即为(ax+by+e)(cx+dy+f)
展开式得
(ax+by+e)(cx+dy+f)=acx2+bdy2+(af+ce)x+(ad+bc)xy+(bf+de)y+ef
由原式原式可知
ac=1①
bd=1②
af+ce=1③
bc+ad=-1④
bf+de=1⑤
ef=0⑥
由①、②式得a=$\frac{1}{c}$,b=$\frac{1}{d}$,
将a、b分别带入④式 得$\frac{c}{d}$+$\frac{d}{c}$=-1,
设$\frac{c}{d}$=m,则m+$\frac{1}{m}$=-1
整理得到m2+m+1=0,
方程m2+m+1=0无解,
故原假设不成立,
故x2-xy+y2+x+y不能分解为两个一次因式的乘积.
点评 此题考查了因式分解的实际运用,熟练掌握多项式乘以多项式法则是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
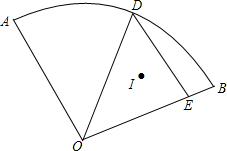 如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$.
如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$.