Question

10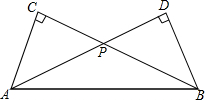．如图，Rt△ABC中，∠ACB=90°，AC=4，BC=8，点P是BC边上的一个动点（不与B，C重合），过点B作射线AP的垂线，D为垂足，设CP=t．
（1）当t=4时，求$\frac{AP}{PD}$的值．
（2）当t为何值时，PA=PB？并求出此时$\frac{AP}{PD}$的值．
（3）用含t的代数式表示$\frac{AP}{PD}$的值．

Answer 1

分析 （1）由已知条件得到PB=8-4=4，根据勾股定理得到AP=4$\sqrt{2}$，通过△APC∽△BPD，根据相似三角形的性质得到$\frac{PC}{PD}=\frac{AP}{PB}$，于是得到结论；
（2）根据勾股定理得到PA=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{{4}^{2}+{t}^{2}}$，由PA=PB，列方程$\sqrt{{4}^{2}+{t}^{2}}$=8-t，解得t=3，通过△APC∽△BPD，根据相似三角形的性质得到$\frac{PC}{PD}=\frac{PA}{PB}$，于是求得结论；
（3）根据勾股定理得到AP=$\sqrt{{4}^{2}+{t}^{2}}$，PB=8-t通过△ACP∽△BPD，根据相似三角形的性质得到$\frac{PC}{PD}=\frac{PA}{PB}$，求出PD=$\frac{t（8-t）}{\sqrt{{4}^{2}+{t}^{2}}}$，即可得到结论．

解答 解：（1）∵CP=4，BC=8，
∴PB=8-4=4，
∵∠ACB=90°，AC=4，
∴AP=4$\sqrt{2}$，
∵∠C=∠D=90°，∠APC=∠BPD
∴△APC∽△BPD，
∴$\frac{PC}{PD}=\frac{AP}{PB}$，
∴$\frac{4}{PD}=\frac{4\sqrt{2}}{4}$，
∴PD=2$\sqrt{2}$，
∴$\frac{AP}{PD}$=$\frac{4\sqrt{2}}{2\sqrt{2}}$=2；

（2）∵CP=t，BC=8，
∴PB=8-t，
∵PA=$\sqrt{A{C}^{2}+P{C}^{2}}$=$\sqrt{{4}^{2}+{t}^{2}}$，
当PA=PB时，$\sqrt{{4}^{2}+{t}^{2}}$=8-t，
解得：t=3，
∴t=3时，PA=PB；
∵t=3，∴PC=3，
∴PA=PB=5，
∵△APC∽△BPD，
∴$\frac{PC}{PD}=\frac{PA}{PB}$，
∴PD=PC=3，
∴$\frac{AP}{PD}$=$\frac{5}{3}$；

（3）∵PC=t，AC=4，BC=8，
∴AP=$\sqrt{{4}^{2}+{t}^{2}}$，PB=8-t，
∵△ACP∽△BPD，
∴$\frac{PC}{PD}=\frac{PA}{PB}$，
∴PD=$\frac{t（8-t）}{\sqrt{{4}^{2}+{t}^{2}}}$，
∴$\frac{PA}{PD}$=$\frac{\sqrt{{4}^{2}+{t}^{2}}}{\frac{t（8-t）}{\sqrt{{4}^{2}+{t}^{2}}}}$=$\frac{16+{t}^{2}}{8t-{t}^{2}}$．

点评 本题考查了相似三角形的判定和性质，勾股定理，证得△ACP∽△BPD是解题的关键，