题目内容
8.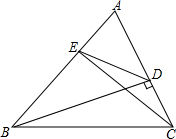 如图,△ABC中,BD⊥AC,CE⊥AB,AD•AE=$\frac{1}{4}$AB•AC,求cosA的值.
如图,△ABC中,BD⊥AC,CE⊥AB,AD•AE=$\frac{1}{4}$AB•AC,求cosA的值.
分析 根据垂直的定义得到∠ADB=∠AEC=90°,由∠A=∠A,推出△ABD∽△ACE,根据相似三角形的性质得到AD:AE=AB:AC,于是得到AD•AC=AE•AB,由于AD•AE=$\frac{1}{4}$AB•AC,两式相除得$\frac{A{E}^{2}}{A{C}^{2}}$-$\frac{1}{4}$,求得$\frac{AE}{AC}$=$\frac{1}{2}$,于是得到cosA=$\frac{AE}{AC}$=$\frac{1}{2}$.
解答 解:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△ACE,
∴AD:AE=AB:AC,
∴AD•AC=AE•AB,
∵AD•AE=$\frac{1}{4}$AB•AC,
∴$\frac{AD•AE}{AD•AC}=\frac{\frac{1}{4}AB•AC}{AE•AB}$,
∴$\frac{A{E}^{2}}{A{C}^{2}}$-$\frac{1}{4}$,
∴$\frac{AE}{AC}$=$\frac{1}{2}$,
∴cosA=$\frac{AE}{AC}$=$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质,余弦函数的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
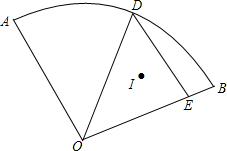 如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$.
如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$.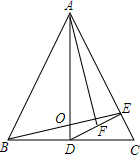 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE. 如图,F是平行四边形ABCD的边CD上的点,FD=2FC,连结AF并延长交BC于E,CE=2,则AD的长为( )
如图,F是平行四边形ABCD的边CD上的点,FD=2FC,连结AF并延长交BC于E,CE=2,则AD的长为( )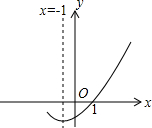 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论正确的有( )个.①a+b+c=0;②ax2+bx+c=0的两根分别为-3和1;③b>2a;④a-2b+c>0.