题目内容
7.已知关于x的一元二次方程x2-ax+2=0的两实数根x1、x2满足x1x2=x1+x2-2.(1)求a的值;
(2)求出该一元二次方程的两实数根.
分析 (1)根据根与系数的关系的关系x1+x2=a,x1x2=2,如何根据x1x2=x1+x2-2得到关于a的方程,解方程即可得到结论;
(2)解方程即可得到结果.
解答 解:(1)∵x1+x2=a,x1x2=2,
又x1x2=x1+x2-2,
∴a-2=2,a=4;
(2)方程可化为x2-4x+2=0,
∴(x-2)2=2,
解得:x-2=$\sqrt{2}$ 或x-2=-$\sqrt{2}$,
∴x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$.
点评 本题考查了根与系数的关系、根的判别式.一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
15.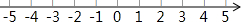 解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
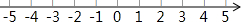 解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{8(x-1)>5x-17}\\{x-6≤\frac{x-10}{2}}\end{array}\right.$并将解集在数轴上表示出来.
12.一种新病毒的直径约为0.00000043毫米,用科学记数法表示为( )
| A. | 0.43×10-6 | B. | 0.43×106 | C. | 4.3×107 | D. | 4.3×10-7 |
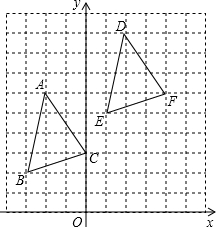 如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.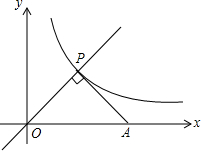 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的交点,PA⊥OP,交x轴于点A,OA=6,则k的值是9.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的交点,PA⊥OP,交x轴于点A,OA=6,则k的值是9.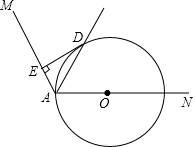 如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E.
如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E. 解不等式x+1<6(x-2)-2,并把它的解集在数轴上表示出来.
解不等式x+1<6(x-2)-2,并把它的解集在数轴上表示出来.