题目内容
18．已知关于x的方程x2-4mx+4m2-9=0．（1）求证：此方程有两个不相等的实数根；
（2）设此方程的两个根分别为x1，x2，其中x1＜x2．若2x1=x2+1，求 m的值．
分析 （1）首先得到△=（-4m）2-4（4m2-9）=36＞0证得方程有两个不相等的实数根；
（2）根据已知条件得到得出关于m的方程求得答案即可．
解答 解：（1）∵△=（-4m）2-4（4m2-9）=36＞0，
∴此方程有两个不相等的实数根；
（2）∵x=$\frac{4m±\sqrt{36}}{2}$=2m±3，
∴x1=2m-3，x2=2m+3，
∵2x1=x2+1，∴2（2m-3）=2m+3+1，
∴m=5．
点评 本题考查了根的判别式的知识，同时题目中还考查了配方法等知识，特别是解决第（2）题时，用公式法求含有字母系数方程更是个难点．
练习册系列答案
名校课堂系列答案
相关题目
已知：∠α，∠β，线段c．
6．
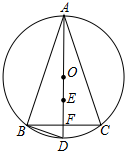已知AD为△ABC的外接圆⊙O的直径，点E是△ABC的内心，AE的延长线交BC于点F，交⊙O于点D，BC=6，cos∠BAC=$\frac{4}{5}$，则EF的长是（ ）
已知AD为△ABC的外接圆⊙O的直径，点E是△ABC的内心，AE的延长线交BC于点F，交⊙O于点D，BC=6，cos∠BAC=$\frac{4}{5}$，则EF的长是（ ）| A． | 1 | B． | 4-$\sqrt{10}$ | C． | 5-$\sqrt{10}$ | D． | $\sqrt{10}$-1 |
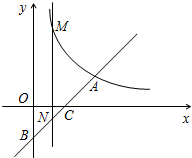如图，在第一象限内，一次函数y=k1x-2的图象与反比例函数y=$\frac{k_2}{x}$的图象相交于点A（4，a），与y轴、x轴分别相交于B，C两点，且BC=CA．