题目内容
17.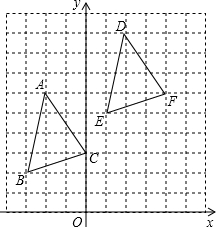 如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
如图,△ABC各顶点的坐标分别为A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.(1)分别写出△DEF各顶点的坐标;
(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
分析 (1)根据横坐标右移加,左移减;纵坐标上移加,下移减即可写出各点的坐标;
(2)连接AD,根据勾股定理求出AD的长,进而可得出结论.
解答 解:(1)∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.
∴D(2,9),E(1,5),F(4,6);
(2)连接AD,∵由图可知,AD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.2015年1-11月绵阳实现对外贸易进出口总值150.4亿元人民币,某新磁公司仓库现有1000吨磁性材料要全部运往A、B两厂,通过了解获得A、B两厂的有关信息如下表(表中运费栏“元/t•km”表示:每吨磁性材料运送一千米所需的费用):
(1)写出总运费y(元)与运往A厂的磁性材料量x(t)之间的函数关系式,并写出自变量的取值范围;
(2)请你运用函数有关知识,为该新磁公司设计总运费最少的运送方案,并求出最少的总运费(可用含a的代数式表示)
| 厂别 | 运费(元/t•km) | 路程(km) | 需求量(t) |
| A | 0.45 | 200 | 不超过650 |
| B | a(a为常数) | 150 | 不超过900 |
(2)请你运用函数有关知识,为该新磁公司设计总运费最少的运送方案,并求出最少的总运费(可用含a的代数式表示)
6.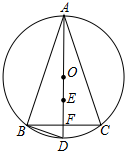 已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
 已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )| A. | 1 | B. | 4-$\sqrt{10}$ | C. | 5-$\sqrt{10}$ | D. | $\sqrt{10}$-1 |
 已知:∠α,∠β,线段c.
已知:∠α,∠β,线段c.