题目内容
5.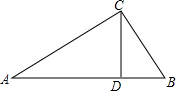 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )| A. | 4 | B. | 16 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
分析 根据相似三角形的性质得到:CD2=AD•BD,把相关线段的长度代入计算即可.
解答 解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,
∴DB=2,∠ADC=∠BDC=90°,
∵∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠DCB,
∴△ACD∽△BCD,
∴$\frac{CD}{BD}=\frac{AD}{CD}$,
∴CD2=BD•AD=2×8=16,
∴CD=4,
故选 A.
点评 本题考查了相似三角形的判定和性质,余角的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目

 如图,△ABC的外角∠DAC的平分线AF交∠ABC的平分线BF于F,BF交AC于E,若∠BAC=80°,∠AEB:∠C=3:2,求∠F的度数.
如图,△ABC的外角∠DAC的平分线AF交∠ABC的平分线BF于F,BF交AC于E,若∠BAC=80°,∠AEB:∠C=3:2,求∠F的度数.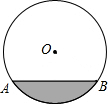 一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度.
一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度. 在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.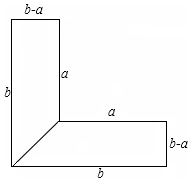 李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.
李红的叔叔在郊区种菜,他家有一块L形菜地,要把L形菜地按如图所示的那样分成面积相等的两个梯形,种上不同的蔬菜.这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米.