题目内容
10.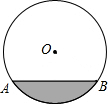 一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度.
一圆柱形排水管的截面如图所示,已知排水管的半径为5m,水面宽AB为8m.由于天气干燥,水管水面下降,此时排水管水面宽变为6m,求水面下降的高度.
分析 先根据垂径定理求得AM、CN,然后根据勾股定理求出OM、ON的长,即可得出结论.
解答 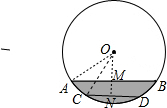 解:如图,下降后的水面宽CD为1.2m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.
解:如图,下降后的水面宽CD为1.2m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.
∴∠ONC=90°.
∵AB∥CD,
∴∠OMA=∠ONC=90°.
∵AB=8,CD=1.2,
∴AM=$\frac{1}{2}$AB=4,CN=$\frac{1}{2}$CD=3,
在Rt△OAM中,
∵OA=5,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=3.
同理可得ON=4,
∴MN=ON-OM=1(米).
答:水面下降了1米.
点评 本题考查的是垂径定理的应用以及勾股定理的应用,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
15.2时整,分针与时针所构成的角的度数是( )
| A. | 40° | B. | 60° | C. | 90° | D. | 180° |
5.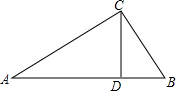 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )| A. | 4 | B. | 16 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |

 一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.