题目内容
8.如图,矩形纸片ABCD中,AD=8,AB=6,现要在矩形纸片中剪出腰长为5的等腰三角形,使点A为等腰三角形一个顶点,一条腰在矩形的边上,要求画出3种不同的等腰三角形,并计算每一种三角形的周长(直接写出结果).
分析 分为两种情况:①当∠A为顶角时,②当∠A为底角时,画出图形,即可得出答案.
解答 解:有两种情况:
①当∠A为顶角时,如图1,此时AE=AF=5,则其△AEF的周长为:5+5+5$\sqrt{2}$=10+5$\sqrt{2}$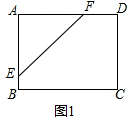
②当∠A为底角时,有两种情况:如图2,
此时AE=EF=5,故BE=1,则BF=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
则AF=$\sqrt{{6}^{2}+(2\sqrt{6})^{2}}$=2$\sqrt{15}$,
故△AEF的周长为:5+5+2$\sqrt{15}$=10+2$\sqrt{15}$. ,
,
如图3,此时AE=EF=5,则DE=3,故DF=4,
则AF=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
故△AEF的周长为:5+5+4$\sqrt{5}$=10+4$\sqrt{5}$.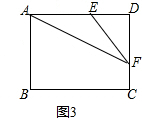 .
.
点评 本题考查了等腰三角形的判定,矩形的性质,勾股定理的应用,能进行分类讨论是解此题的关键.

练习册系列答案
相关题目
5.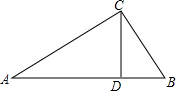 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,AB=10,则CD长为( )| A. | 4 | B. | 16 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
 如图所示,已知∠α和∠β,利用尺规作∠BOD=∠α+∠β.
如图所示,已知∠α和∠β,利用尺规作∠BOD=∠α+∠β. 一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
一座隧道的截面由抛物线和长方形组成,长方形的长为8m,宽为2m,隧道的最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.