题目内容
10.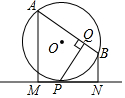 如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.
如图,MN切⊙O的弦于P,AB是⊙O的弦,AM⊥MN于M,BN⊥MN于N,PQ⊥AB于Q,求证:PQ2=AM•BN.
分析 连接AP,BP,根据垂直的定义得到∠AMP=∠PQB=90°,根据相似三角形的性质得到$\frac{PQ}{AM}$=$\frac{BN}{PQ}$,同理可得:$\frac{PB}{PA}$=$\frac{BN}{PQ}$,等量代换得到$\frac{PQ}{AM}=\frac{BN}{PQ}$,于是得到结论.
解答 证明:连接AP,BP,
∵AM⊥MN于M,PQ⊥AB于Q.
∴∠AMP=∠PQB=90°,
∵∠1=∠2,
∴△PAM∽△BPQ,
∴$\frac{PQ}{AM}$=$\frac{BN}{PQ}$,
同理可得:$\frac{PB}{PA}$=$\frac{BN}{PQ}$,
∴$\frac{PQ}{AM}=\frac{BN}{PQ}$,
∴PQ2=AM•BN.
点评 本题考查了和圆有关的比例线段的证明题,可由所要证的比例式找到相似三角形;当要证明的比例式不能直接应用有关定理和相似三角形来证明时,可以考虑等量代换.等量代换通常有等线段代换、等比代换等.

练习册系列答案
相关题目
1.同一时刻,身高1.72m的小明在阳光下影长为0.86米;小宝在阳光下的影长为0.64m,则小宝的身高为( )
| A. | 1.28m | B. | 1.13m | C. | 0.64m | D. | 0.32m |
5.不等式组$\left\{\begin{array}{l}{-3(x+1)-x<5}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$的解为( )
| A. | x<-2或x≥1 | B. | x<-2 | C. | -2<x≤1 | D. | -2$<x<\frac{1}{2}$ |
15.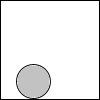 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )| A. | a2-π | B. | 4-π | C. | π | D. | (4-π)a2 |
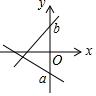

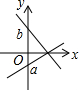

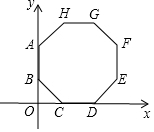 如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).
如图,正八边形的边长为2,点C的坐标是($\sqrt{2}$,0).