题目内容
5．不等式组$\left\{\begin{array}{l}{-3（x+1）-x＜5}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1}\end{array}\right.$的解为（ ）| A． | x＜-2或x≥1 | B． | x＜-2 | C． | -2＜x≤1 | D． | -2$＜x＜\frac{1}{2}$ |
分析 先求出每个不等式的解集，再求出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{-3（x+1）-x＜5①}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1②}\end{array}\right.$
∵解不等式①得：x＞-2，
解不等式②得：x≤1，
∴不等式组的解集为-2＜x≤1，
故选C．
点评 本题考查了解一元一次不等式组的应用，能根据不等式的解集求出不等式组的解集是解此题的关键．
练习册系列答案
相关题目
如图，⊙O1和⊙O2相交于A、B，C为⊙O1上一点，CA交⊙O2于D，BD交⊙O1于F，直线CF交⊙O2于E、G．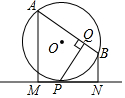
如图，MN切⊙O的弦于P，AB是⊙O的弦，AM⊥MN于M，BN⊥MN于N，PQ⊥AB于Q，求证：PQ2=AM•BN．