题目内容
12．
如图在△ABC中，AB=AC，∠A=120°，BC=9cm，AB的垂直平分线交BC于点M，交AB于点N，AC的垂直平分线交BC于点E，交AC于点F，则ME的长是（ ）| A． | 2cm | B． | 3cm | C． | 4cm | D． | 5cm |
分析 首先连接AM，AE，由在△ABC中，AB=AC，∠A=120°，可求得∠B=∠C=30°，又由AB的垂直平分线交BC于点M，交AB于点N，AC的垂直平分线交BC于点E，交AC于点F，易得△AME是等边三角形，继而求得答案．
解答 解：连接AM，AE，
∵在△ABC中，AB=AC，∠A=120°，
∴∠C=∠B=30°，
∵AB的垂直平分线交BC于点M，交AB于点N，AC的垂直平分线交BC于点E，交AC于点F，
∴AE=CE，AM=BM，
∴∠CAE=∠C=30°，∠BAM=∠B=30°，
∴∠AEM=∠AME=60°，
∴△AME是等边三角形，
∴AM=AE=MN，
∴BM=ME=CE，
∵BC=9cm，
∴ME=3cm．
故选：B．．
点评 此题考查了线段垂直平分线的性质以及等边三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
3．a、b为实数，且ab=1，设P=$\frac{a}{a+1}$+$\frac{b}{b+1}$，Q=$\frac{1}{a+1}$+$\frac{1}{b+1}$，则P与Q的大小关系（ ）
| A． | P=Q | B． | P＜Q | C． | P＞Q | D． | 无法确定 |
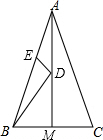如图，△ABC中，AB=AC=4，∠BAC=45°，AM平分∠BAC，点D、E 分别为AM、AB上的动点，则BD+DE的最小值是2$\sqrt{2}$．
正方形ABCD，正方形CEFG如图放置，点B、C、E在同一条直线上，点P在BC边上，PA=PF，且∠APF=90°，连接AF交CD于点M．有下列结论：①EC=BP；②AP=AM：③∠BAP=∠GFP；④AB2+CE2=$\frac{1}{2}$AF2；⑤S正方形ABCD+S正方形CGFE=2S△APF，其中正确的是（ ）