题目内容
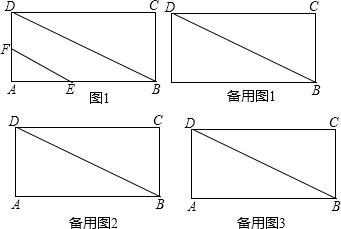
11.在四边形ABCD中,∠ABC+∠ADC=180°,CB=CD.(1)如图1,求证:AC平分∠BAD;
(2)如图2,连接BD交AC于点E,在AB延长线上取一点M(点M不在直线CD上),连接MC,过D作DN⊥BD交MC延长线于点N,若∠ABD=90°,试探究线段AD、AM、DN之间的数量关系,并说明理由.
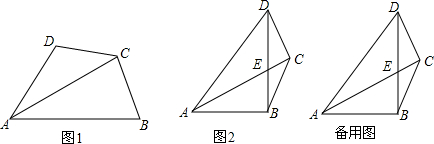
分析 (1)先证明A、B、C、D四点共圆,由CB=CD,得出$\widehat{CB}=\widehat{CD}$,得出∠BAC=∠DAC,即可得出结论;
(2)分两种情况:①在AD上截取AF=AM,连接CF,先证明△ACF≌△ACM,得出∠AFC=∠AMC,得出∠CFD=∠1,由A、B、C、D四点共圆,得出∠ACD=∠ABD=90°,∠DAC=∠BDC再证明△CDF≌△CDN,得出DF=DN,即可得出结论;②解法同①.
解答 (1)证明:∵∠ABC+∠ADC=180°,
∴A、B、C、D四点共圆,
∵CB=CD,
∴$\widehat{CB}=\widehat{CD}$,
∴∠BAC=∠DAC,
即AC平分∠BAD;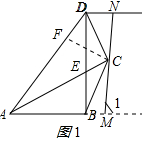
(2)解:分两种情况:
①如图1所示:AD=AM+DN;理由如下:
在AD上截取AF=AM,连接CF,
在△ACF和△ACM中,$\left\{\begin{array}{l}{AF=AM}&{\;}\\{∠CAF=∠CAM}&{\;}\\{AC=AC}&{\;}\end{array}\right.$,
∴△ACF≌△ACM(SAS),
∴∠AFC=∠AMC,
∴∠CFD=∠1,
∵A、B、C、D四点共圆,
∴∠ACD=∠ABD=90°,∠DAC=∠BDC,
∴∠ADC+∠DAC=90°,
∵DN⊥BD,∠ABD=90°,
∴∠BDN=90°,DN∥AM,
∴∠CDN+∠BDC=90°,∠CND=∠1,
∴∠ADC=∠CDN,∠CFD=∠CND,
在△CDF和△CDN中,$\left\{\begin{array}{l}{∠CFD=∠CND}&{\;}\\{∠CDF=∠CDN}&{\;}\\{CD=CD}&{\;}\end{array}\right.$,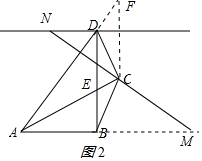
∴△CDF≌△CDN(AAS),
∴DF=DN,
∴AF+DF=AM+DN,
即AD=AM+DN;
②如图2所示:AD=AM-DN;理由如下:
在AD上截取AF=AM,连接CF,
同①得:DF=DN,
∵AD+DF=AM,
∴AD=AM-DN.
点评 本题考查了四点共圆、全等三角形的判定与性质、圆周角定理、平行线的判定与性质;证明三角形全等和四点共圆是解决问题的关键.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案 如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.
如图,有一个直角三角形纸片,两直角边AC=5cm,BC=12cm,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是( )cm.| A. | 3 | B. | 4 | C. | $3\frac{1}{3}$ | D. | $4\frac{2}{3}$ |
 如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧$\widehat{BD}$的度数是( )
如图,四边形ABCD内接于⊙O,∠A=100°,则劣弧$\widehat{BD}$的度数是( )| A. | 80° | B. | 100° | C. | 130° | D. | 160° |
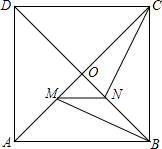 如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.
如图,在正方形ABCD中,对角线AC、BD交于点O,MN∥AB,分别与OA、OB交于点M、N,连接BM、CN,猜测线段BM与CN的大小及位置关系?证明你的猜测.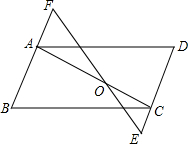 如图,已知AB=CD,AD=BC,O为AC上任意一点,过O点作直线分别交BA,DC的延长线于点F,E,求证:∠E=∠F.
如图,已知AB=CD,AD=BC,O为AC上任意一点,过O点作直线分别交BA,DC的延长线于点F,E,求证:∠E=∠F.