题目内容
16.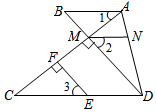 如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
分析 首先证明EF∥DM可得∠3=∠CDM,进而可得∠2=∠CDM,可证明MN∥CD,再根据平行线的性质可得∠AMN=∠C,结合已知条件再证明AB∥MN.
解答 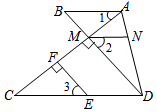 证明:∵EF⊥AC,DM⊥AC,
证明:∵EF⊥AC,DM⊥AC,
∴∠CFE=∠CMD=90°(垂直定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等),
∵∠3=∠2(已知),
∴∠2=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠AMN=∠C(两直线平行,同位角相等),
∵∠1=∠C(已知),
∴∠1=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行).
点评 此题主要考查了平行线的判定和性质,关键是掌握内错角相等,两直线平行.两直线平行,内错角相等.

练习册系列答案
相关题目
11. 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )
 三个正方形的面积如图,正方形A的面积为( )
三个正方形的面积如图,正方形A的面积为( )| A. | 6 | B. | 4 | C. | 64 | D. | 8 |
1.为了解学生的身高情况,抽测了某校17岁的50名男生的身高,将数据分成7组,列出了相应的频数分布表(部分未列出)如下:
某校50名17岁男生身高的频数分布表
请回答下列问题:
(1)请将上述频数分布表填写完整;
(2)估计这所学校17岁男生中,身高不低于1.655m且不高于1.715m的学生所占的百分比;
(3)该校17岁男生中,身高在哪个范围内的频数最多?如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人?
某校50名17岁男生身高的频数分布表
| 分 组(m) | 频数(名) | 频率 |
| 1.565~1.595 | 2 | 0.04 |
| 1.595~1.625 | 4 | 0.08 |
| 1.6254~1.655 | 6 | 0.12 |
| 1.655~1.685 | 11 | 0.22 |
| 1.685~1.715 | 17 | 0.34 |
| 1.715~1.745 | 6 | 0.12 |
| 1.745~1.775 | 4 | 0.08 |
| 合 计 | 50 | 1 |
(1)请将上述频数分布表填写完整;
(2)估计这所学校17岁男生中,身高不低于1.655m且不高于1.715m的学生所占的百分比;
(3)该校17岁男生中,身高在哪个范围内的频数最多?如果该校17岁男生共有350名,那么在这个身高范围内的人数估计有多少人?
8.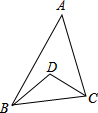 如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
 如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )
如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC=( )| A. | 110° | B. | 100° | C. | 90° | D. | 80° |
6.下列四个函数:①y=-2x+1,②y=3x-2,③y=-$\frac{3}{x}$,④y=x2+2,当x>0时,y随x的增大而增大的函数是( )
| A. | ①②③ | B. | ①③④ | C. | ②③④ | D. | ②④ |
 如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.
如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.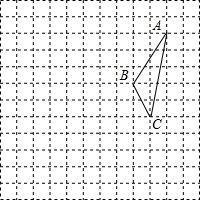 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)