题目内容
5.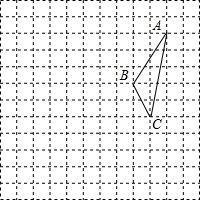 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)(1)请作出△ABC中BC边上的高线AD;(D点不一定在格点上)
(2)请在如图所示的网格平面内作出平面直角坐标系;(要求标注出原点O、x轴和y轴)
(3)若平移△ABC,使点A落在A′(-1,5),请作出平移后的△A′B′C′.
分析 (1)利用钝角三角形高线的做法得出答案;
(2)直接利用A,C点坐标建立平面直角坐标系即可;
(3)直接利用平移的性质得出对应点位置进而得出答案.
解答  解:(1)如图所示:线段AD为BC边上的高线;
解:(1)如图所示:线段AD为BC边上的高线;
(2)如图画出平面直角坐标系;
(3)如图所示:△A′B′C′即为所求.
点评 此题主要考查了平移变换以及三角形高线的做法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | x7÷x5=x2 | B. | 2a2+4a2=6a4 | C. | (a2)3=a5 | D. | (x+1)2=x2+1 |
17.下面四个多项式中,能进行因式分解的是( )
| A. | x2+y2 | B. | x2-y | C. | x2-1 | D. | x2+x+1 |
14.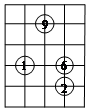 如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋
如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋 的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )
的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )
 如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋
如图是一局围棋比赛的几手棋,为记录棋谱方便,模线用数字表示,纵线用字母表示,这样,黑棋 的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )
的位置可记为(B,20),白棋②的位置可记为(D,19),则白棋⑨的位置应记为( )| A. | (C,24) | B. | (24,C) | C. | (C,22) | D. | (22,C) |
15.已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=-3m}\\{x-y=4+m}\end{array}\right.$满足x>0且y<0,则m的取值范围是( )
| A. | m>1 | B. | m<2 | C. | -1<m<2 | D. | 1<m<2 |
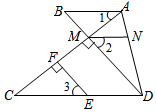 如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN.
如图,已知:EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明AB∥MN. 如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.