题目内容
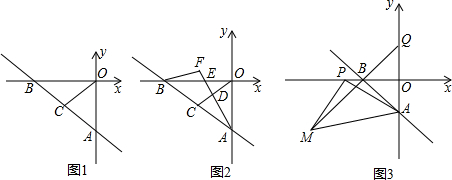
10.如图,在Rt△ABC,∠C=90°,点O在斜边AB上,以O为圆心,OA为半径的⊙O与直角边BC相切于点D.(1)求证:AD平分∠BAC;
(2)若CD=3,BD=5,求AC的长;
(3)如图,若直线BC向上平移后交⊙O于点D.E,⊙O交AB于点F,求证:∠CAD=∠BAE.

分析 (1)连接OD.由切线的性质可知:OD⊥BC,从而可得到DO∥AC,由平行线的性质可知∠ODA=∠DAC,然后由∠ODA=∠OAD可得到∠OAD=∠DAC,故此AD平分∠BAC;
(2)过点D作DE⊥AB,垂足为E.由角平分线的性质可知DE=DC=3,然后利用HL可证明Rt△AED≌Rt△ACD,从而可知AE=AC,在Rt△BDE中,由勾股定理可知BE=4,设AC=AE=x,则AB=4+x,在Rt△ABC中由勾股定理得(x+4)2=x2+82,解得x=6,从而得到AC=6;
(3)如图3所示,连接EF.由直角所对的圆周等于90度可得到∠FEA=∠C,由圆内接四边形的性质可知∠AFE=∠ADE,根据三角形的内角和定理可知∠CAD=∠FAE.
解答 解:(1)连接OD.
∵BC是圆O的切线,
∴OD⊥BC.
∵∠AC⊥BC,
∴DO∥AC.
∴∠ODA=∠DAC.
∵OD=OA,
∴∠ODA=∠OAD.
∴∠OAD=∠DAC.
∴AD平分∠BAC.
(2)过点D作DE⊥AB,垂足为E.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC=3.
在Rt△AED和Rt△ACD中,
$\left\{\begin{array}{l}{ED=DC}\\{AD=AD}\end{array}\right.$,
∴Rt△AED≌Rt△ACD.
∴AE=AC.
在Rt△BDE中,BE=$\sqrt{B{D}^{2}-D{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4.
设AC=AE=x,则AB=4+x.
在Rt△ABC中,AB2=AC2+CB2,即(x+4)2=x2+82.
解得:x=6.
∴AC=6.
(3)如图3所示,连接EF.
∵AF是圆O的直径,
∴∠FEA=90°.
∴∠FEA=∠C.
∵四边形FEDA是圆内接四边形,
∴∠AFE=∠ADE.
∴∠CAD=∠FAE.
点评 本题主要考查的是切线的性质、角平分线的性质、全等三角形的性质和判定、勾股定理的应用,圆内接四边形的性质、圆周角定理的应用,掌握本题的辅助线的作法是解题的关键.

| 试验次数 | 20 | 40 | 60 | 80 | 100 |
| “和为2”的频数 | 6 | 8 | 14 | 24 | 27 |
| “和为2”的频率 | 0.30 | 0.20 | 0.23 | 0.30 | 0.27 |
| 试验次数 | 120 | 140 | 160 | 180 | 200 |
| “和为2”的频数 | 28 | 38 | 42 | 46 | 49 |
| “和为2”的频率 | 0.23 | 0.27 | 0.26 | 0.27 | 0.25 |
(2)请你根据试验数据求事件“和为2”的概率;
(3)你能通过直接计算分别求得事件“和为2”、“和为3”、“和为4”的概率吗?试试看.
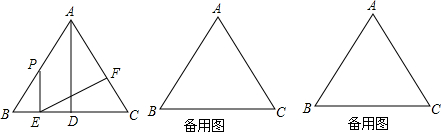
 如图所示,在△ABC中,∠B=45°,AC=5,BC=3,求sinA和AB.
如图所示,在△ABC中,∠B=45°,AC=5,BC=3,求sinA和AB.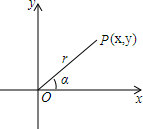 如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.
如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.