题目内容
19.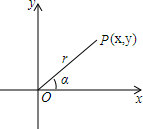 如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.
如图,在平面直角坐标系的第一象限内有一点p(x,y),点P到原点的距离OP=r,且PO与x轴的正半轴成α角.(1)用x,y,r表示角α的正弦和余弦;
(2)求sin2α+cos2α的值,通过计算你有何发观?
(3)用x,y,r表示角90°-α的正弦和余弦,并与角α的正弦和余弦作比较.你又有何发观?
分析 (1)作PH⊥x轴于H,如图,由P点坐标得OH=x,PH=y,然后在Rt△OPH,利用正弦和余弦的定义易得sinα=$\frac{y}{r}$,cosα=$\frac{x}{r}$;
(2)由于sin2α+cos2α=$\frac{{x}^{2}+{y}^{2}}{{r}^{2}}$,利用勾股定理得到x2+y2=r2,所以sin2α+cos2α=1,于是可判断一个锐角的正弦和余弦的平方和等于1;
(3)利用正弦与余弦的定义易得cos(90°-α)=$\frac{y}{r}$,sin(90°-α)=$\frac{x}{r}$,即sinα=cos(90°-α),cosα=sin(90°-α).
解答 解:(1)作PH⊥x轴于H,如图,
∵P点坐标为(x,y),
∴OH=x,PH=y,
在Rt△OPH,sin∠POH=$\frac{y}{r}$,cos∠POH=$\frac{x}{r}$,
即sinα=$\frac{y}{r}$,cosα=$\frac{x}{r}$;
(2)sin2α+cos2α=($\frac{y}{r}$)2+($\frac{x}{r}$)2=$\frac{{x}^{2}+{y}^{2}}{{r}^{2}}$,
而OH2+PH2=OP2,即x2+y2=r2,
∴sin2α+cos2α=1,
即一个锐角的正弦和余弦的平方和等于1;
(3)在Rt△OPH,cos∠OPH=$\frac{y}{r}$,sin∠OPH=$\frac{x}{r}$,
即cos(90°-α)=$\frac{y}{r}$,sin(90°-α)=$\frac{x}{r}$,
∴sinα=cos(90°-α),cosα=sin(90°-α).
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和锐角三角函数的定义.

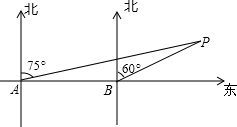 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=( )| A. | 7海里 | B. | 14海里 | C. | 3.5海里 | D. | 4海里 |
| A. | -$\frac{1}{343}$ | B. | -$\frac{1}{21}$ | C. | -343 | D. | -21 |

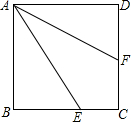 如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.
如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.