题目内容
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 作直径BD,连接CD,作OH⊥BC于H,根据垂径定理和三角形中位线定理求出CD,根据勾股定理求出BC,根据正切的概念计算即可.
解答 解: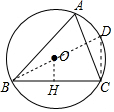 作直径BD,连接CD,作OH⊥BC于H,
作直径BD,连接CD,作OH⊥BC于H,
则OH=3,BH=HC,
∵BO=OD,BH=HC,
∴CD=2OH=6,
∵BD为直径,
∴∠BCD=90°,
由勾股定理得,BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=8,
∴tanD=$\frac{BC}{CD}$=$\frac{4}{3}$,
∵∠D=∠A,
∴tanA=$\frac{4}{3}$,
故选:A.
点评 本题考查的是三角形的外接圆和外心、垂径定理和勾股定理,掌握正切的概念、圆周角定理是解题的关键.

练习册系列答案
相关题目
5.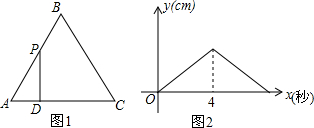 如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )
如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )
 如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )
如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
3.调查显示,截止2016年底某市汽车拥有量为16.9万辆,已知2014年底该市汽车拥有量为10万辆,设2014年底至2016年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
5.若a与-5互为相反数,则a的值是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
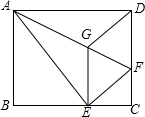 如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.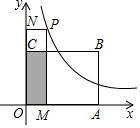 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
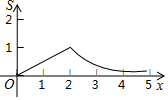
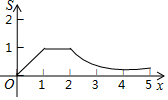
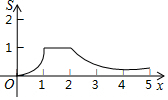
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )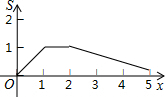
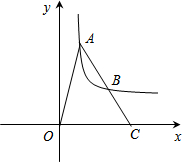 如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点,则△OAC的面积为( )
如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点,则△OAC的面积为( )
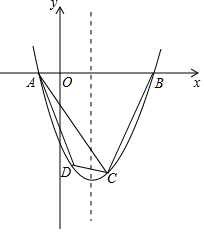 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).