题目内容
10.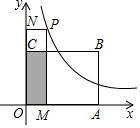 如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )
如图,矩形OABC的四个顶点分别为O(0,0),A(2,0),B(2,1),C(0,1),P(x,y)是反比例函数y=$\frac{1}{x}$(x>0)图象上的一个动点,过点P作PM⊥x轴,PN⊥y轴,M、N为垂足,记矩形OMPN与矩形OABC的重叠部分面积为S,则S与x轴的函数关系式的图象为( )| A. | 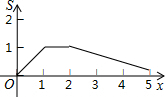 | B. | 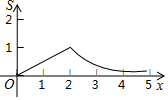 | ||
| C. | 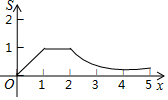 | D. | 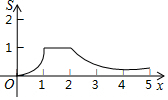 |
分析 分三种情况,分别求出S与x的函数关系式,即可得出结论.
解答 解:∵A(2,0),B(2,1),C(0,1),
∴OA=BC=2,AB=OC=1,
分三种情况:
①当0<x≤1时,S=x;
②当1<x≤2时,S=xy=1;
③当x>2时,S=2y=$\frac{2}{x}$;
由函数的图象得:选项C正确;
故选:C.
点评 此题主要考查了动点问题的函数图象、反比函数的综合应用以及矩形面积求法等知识,正确利用数形结合以及分类讨论求出函数关系式是解题关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
1.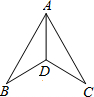 如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
 如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )
如图,已知∠BAD=∠CAD,图中再补充一个条件后不能说明△ABD≌△ACD,则这个条件是( )| A. | AB=AC | B. | ∠B=∠C | C. | BD=CD | D. | ∠ADB=∠ADC |
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
19.某班学校毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了2550份留言,如果全班有x名学生,根据题意,列出方程( )
| A. | $\frac{x(x-1)}{2}$=2550 | B. | $\frac{x(x+1)}{2}$=2550 | C. | x(x-1)=2550 | D. | x(x+1)=2550 |
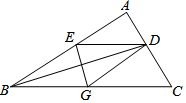 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
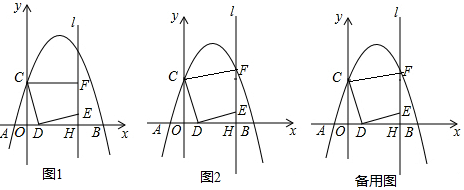
 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)