题目内容
3.调查显示,截止2016年底某市汽车拥有量为16.9万辆,已知2014年底该市汽车拥有量为10万辆,设2014年底至2016年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
分析 根据年平均增长率相等,可以得到2014年的汽车拥有量乘(1+x)2,即可得到2016年的汽车拥有量,从而可以写出相应的方程,从而可以解答本题.
解答 解:由题意可得,
10(1+x)2=16.9.
故选:A.
点评 本题考查由实际问题抽象出一元二次方程,解答此类问题的关键是明确题意,写出相应的方程.

练习册系列答案
相关题目
14.从一个多边形的一个顶点引出的对角线把多边形分成了10个三角形,则这个多边形一共有( )条对角线.
| A. | 54 | B. | 45 | C. | 35 | D. | 27 |
11.将2.05×10-3用小数表示为( )
| A. | 0.000205 | B. | 0.00205 | C. | 0.0205 | D. | -0.00205 |
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
13.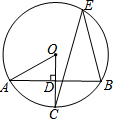 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |

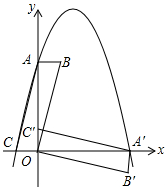 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.