题目内容
20.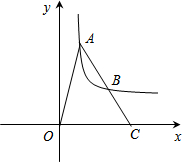 如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点,则△OAC的面积为( )
如图,A、B是双曲线y=$\frac{k}{x}$上的点,点A的坐标是(1,4),B是线段AC的中点,则△OAC的面积为( )| A. | 6 | B. | 4 | C. | 10 | D. | 12 |
分析 首先把A的坐标代入反比例函数的一般形式求得k的值,根据A的坐标求得B的纵坐标为2,代入y=$\frac{4}{x}$求得x=2,即可求得B的坐标,最后根据A、B的坐标求得直线AB的解析式,求得C的坐标,然后根据三角形面积公式即可求得.
解答 解:把A(1,4)代入y=$\frac{k}{x}$得4=$\frac{k}{1}$,
解得k=4;
由B是AC的中点可得B点的纵坐标是A点纵坐标的一半,即y=2,
把y=2代入y=$\frac{4}{x}$求得x=2,故B点的坐标为(2,2);
由A、B点的坐标求得直线AB的解析式为y=-2x+6,
令y=0,求得x=3,
∴C点的坐标为(3,0)
∴△OAC的面积为$\frac{1}{2}$×3×4=6.
故选A.
点评 本题考查了待定系数法求反比例函数和一次函数的解析式的解析式,反比例函数图象上点的坐标特征,三角形面积等,求得B点的坐标是解题的关键.

练习册系列答案
相关题目
11.将2.05×10-3用小数表示为( )
| A. | 0.000205 | B. | 0.00205 | C. | 0.0205 | D. | -0.00205 |
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
10.面积为2的正方形的边长在( )
| A. | 1.5和2之间 | B. | 1和1.5之间 | C. | 0.5和1之间 | D. | 0和0.5之间 |
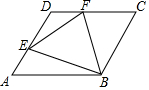 己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图象是( )
己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图象是( )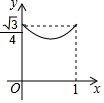
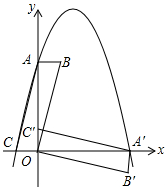 在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.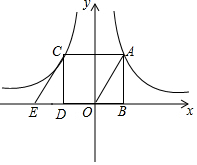 在平面直角坐标系中,把图中的Rt△ABO(∠ABO=90°)沿x轴负半轴平移得到△CDE,已知OB=3,AB=4,函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过点A.
在平面直角坐标系中,把图中的Rt△ABO(∠ABO=90°)沿x轴负半轴平移得到△CDE,已知OB=3,AB=4,函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过点A.