题目内容
4.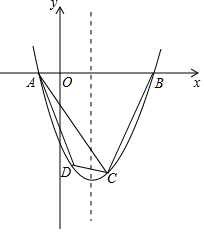 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).(1)求该抛物线的解析式和点A的坐标;
(2)点D(m,n)(-1<m<2)在抛物线图象上,当△ACD的面积为$\frac{27}{8}$时,求点D的坐标;
(3)在(2)的条件下,设抛物线的对称轴为l,点D关于l的对称点为E,能否在抛物线图象和l上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
分析 (1)由B、C三点的坐标,利用待定系数法可求得抛物线的解析式,进而求出点A的坐标;
(2)过D作DH垂直x轴于H,CG垂直x轴于G.则S△ACD=S△ADH+S四边形HDCG-S△ACG,进而求出D点坐标;
(3)由D点坐标,可求得DE的长,当DE为边时,根据平行四边形的性质可得到PQ=DE=2,从而可求得P点坐标;当DE为对角线时,可知P点为抛物线的顶点,可求得P点坐标.
解答 解:(1)∵抛物线y=x2+bx+c经过B、C二点,且B(4,0),C(2,-6),
∴$\left\{\begin{array}{l}{16+4b+c=0}\\{4+2b+c=-6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-3}\\{c=4}\end{array}\right.$,
∴该抛物线的解析式:y=x2-3x-4,
∵抛物线y=x2-3x-4经过点A,且点A在x轴上
∴x2-3x-4=0,解得:x1=-1或x2=4(舍去)
∴点A的坐标(-1,0);
(2)如图1,过D作DH垂直x轴于H,CG垂直x轴于G.
∵点D(m,n)(-1<m<2),C(2,-6)
∴点H(m,0),点G(2,0).
则S△ACD=S△ADH+S四边形HDCG-S△ACG,
=$\frac{1}{2}$|n|(m+1)+$\frac{1}{2}$(|n|+6)(2-m)-$\frac{1}{2}$(|-1|+2)×|-6|
=$\frac{3}{2}$|n|-3m-3,
∵点D(m,n)在抛物线图象上,
∴n=m2-3m-4,
∵-1<m<2,即m2-3m-4<0
∴|n|=4+3m-m2,
∵△ACD的面积为:$\frac{27}{8}$,
∴$\frac{3}{2}$(4+3m-m2)-3m-3=$\frac{27}{8}$
即4m2-4m+1=0,
解得m=$\frac{1}{2}$.
∴D($\frac{1}{2}$,$-\frac{21}{4}$).
(3)能.理由如下:
∵y=x2-3x-4=${(x-\frac{3}{2})^2}-\frac{25}{4}$,
∴抛物线的对称轴l为$x=\frac{3}{2}$.
∵点D关于l的对称点为E,
∴E($\frac{5}{2}$,-$\frac{21}{4}$),∴DE=$\frac{5}{2}$-$\frac{1}{2}$=2.
①当DE为平行四边形的一条边时,如图2:
则PQ∥DE且PQ=DE=2.
∴点P的横坐标为$\frac{3}{2}$+2=$\frac{7}{2}$或$\frac{3}{2}$-2=-$\frac{1}{2}$.
∴点P的纵坐标为($\frac{7}{2}$-$\frac{3}{2}$)2-$\frac{25}{4}$=-$\frac{9}{4}$.
∴点P的坐标为($\frac{7}{2}$,-$\frac{9}{4}$)或(-$\frac{1}{2}$,-$\frac{9}{4}$),
②当DE为平行四边形的一条对角线时,对角线PQ、DE互相平分,由于Q在抛物线对称轴上,对称轴l垂直平分DE,因此点P在对称轴与抛物线的交点上,即为抛物线顶点($\frac{3}{2}$,-$\frac{25}{4}$).
综上所述,存在点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形,点P的坐标为($\frac{7}{2}$,-$\frac{9}{4}$)或(-$\frac{1}{2}$,-$\frac{9}{4}$)或($\frac{3}{2}$,-$\frac{25}{4}$).
点评 本题主要考查二次函数综合应用,涉及待定系数法、勾股定理、平行四边形的性质等知识点.在(1)中注意二次函数解析式三种形式的灵活运用,在(3)中求得D点的坐标从而求得DE的长是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 54 | B. | 45 | C. | 35 | D. | 27 |
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
| A. | $\frac{x(x-1)}{2}$=2550 | B. | $\frac{x(x+1)}{2}$=2550 | C. | x(x-1)=2550 | D. | x(x+1)=2550 |
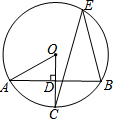 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
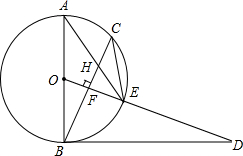 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC. 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.
菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.