题目内容
7.如图1,在矩形ABCD中,动点P从点B出发,沿BC→CD→DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,则m的值是( )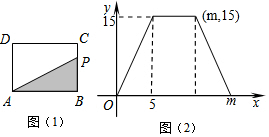
| A. | 6 | B. | 8 | C. | 11 | D. | 16 |
分析 首先结合题意可得当点P运动到点C,D之间时,△ABP的面积不变,则可得当BC=5,CD=6,继而求得答案.
解答 解:动点P从点B出发,沿BC、CD、DA运动至点A停止,
∵当点P运动到点C,D之间时,△ABP的面积不变.函数图象上横轴表示点P运动的路程,
∴x=5时,y开始不变,说明BC=5,
∴△ABC的面积为:y=$\frac{1}{2}$×AB×5=15.
∴AB=6,
∵四边形ABCD为矩形,
∴CD=AB=6,
∴M=5+6=11.
故选:C.
点评 本题考查了动点问题的函数图象.注意解决本题应首先看清横轴和纵轴表示的量,找到面积不变的开始与结束,得到BC,CD的具体值.

练习册系列答案
相关题目
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
19.某班学校毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了2550份留言,如果全班有x名学生,根据题意,列出方程( )
| A. | $\frac{x(x-1)}{2}$=2550 | B. | $\frac{x(x+1)}{2}$=2550 | C. | x(x-1)=2550 | D. | x(x+1)=2550 |
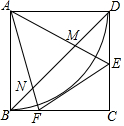 如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )
如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )
 在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-1与x轴交于A,B两点(点A在点B左侧)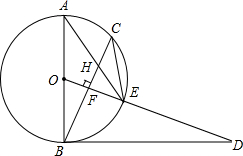 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.