题目内容
5.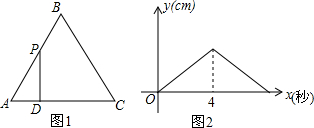 如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )
如图1,在等边三角形△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止,过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5.5秒时,PD的长是( )| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
分析 由题意和等边三角形的性质得出AB=BC=4,∠C=60°,再由三角函数即可求出PD的长.
解答 解:根据题意得:AB=4,
∵△ABC是等边三角形,
∴AB=BC=4,∠C=60°, 当点P运动5.5秒时,如图所示:
当点P运动5.5秒时,如图所示:
则BP=5.5-4=1.5,
∴PC=2.5,
∴PD=PC•sin60°=2.5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$;
故选:A.
点评 本题考查了动点问题的函数图象、等边三角形的性质、三角函数的运用;熟练掌握等边三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
16.抛物线y=ax2与直线x=1,x=3,y=1,y=2围成的长方形有公共点,则实数a的取值范围( )
| A. | $\frac{1}{9}$≤a≤1 | B. | $\frac{1}{9}$≤a≤2 | C. | $\frac{1}{3}$≤a≤1 | D. | $\frac{1}{3}$≤a≤2 |
14.从一个多边形的一个顶点引出的对角线把多边形分成了10个三角形,则这个多边形一共有( )条对角线.
| A. | 54 | B. | 45 | C. | 35 | D. | 27 |
15. 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
 如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )
如图,△ABC内接于半径为5的圆心O,圆心O到弦BC的距离等于3,则tanA等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
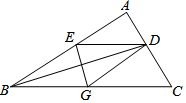 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.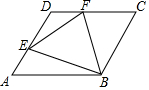 己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图象是( )
己知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设△BEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图象是( )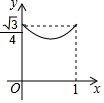
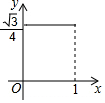
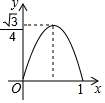
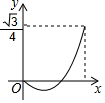
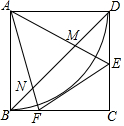 如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )
如图,正方形ABCD中,点E,F分别在边CD,BC上,且∠EAF=45°,BD分别交AE,AF于点M,N,以点A为圆心,AB长为半径画弧BD.下列结论:①DE+BF=EF;②BN2+DM2=MN2;③△AMN∽△AFE;④$\widehat{BD}$与EF相切;⑤EF∥MN.其中正确结论的个数是( )