题目内容
12.已知正六边形的边心距为3,则它的周长为12$\sqrt{3}$.分析 连接OA、OB,作OC⊥AB于C,由正六边形的性质得出AC=BC=$\frac{1}{2}$AB,∠AOB=60°,得出∠AOC=30°,由三角函数求出AC,得出AB,即可求出正六边形的周长.
解答 解:如图所示: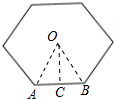
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=$\frac{1}{2}$AB,∠AOB=60°,
∴∠AOC=30°,
∴AC=$\frac{\sqrt{3}}{3}$OC=$\frac{\sqrt{3}}{3}$×3=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
∴正六边形的周长=6AB=12$\sqrt{3}$.
故答案为:12$\sqrt{3}$.
点评 本题考查了正多边形和圆、正六边形的性质、三角函数等知识;熟练掌握正六边形的性质,运用三角函数求出AC是解决问题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
3.观察下列图形,它们是按一定规律排列,依照此规律,第5个图形有( )个五角星.


| A. | 24 | B. | 32 | C. | 21 | D. | 19 |
20.下列说法正确的有( )①最大的负整数是-1;②绝对值等于本身的数是正数;③有理数分为正有理数、负有理数和零;④数轴上表示-a的点一定在原点的左边;⑤在数轴上7与9之间的有理数是8.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.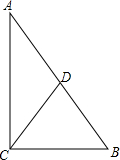 如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )
如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )
 如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )
如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
4.已知点(m-1,n+2)与(2m-4,2)关于x轴对称,则(m+n)2015的值是( )
| A. | 1 | B. | -1 | C. | 2013 | D. | -2013 |
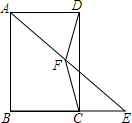 如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.
如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.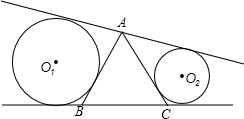 如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.