题目内容
7.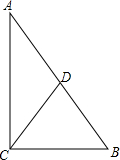 如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )
如图,在直角△ABC中,∠C=90°,CD是斜边AB的中线,若CD=2,AC=3,则sinB的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
分析 根据在直角△ABC中,∠C=90°,CD是斜边AB的中线,可得AB=2CD,由CD=2,AC=3,可得AB的长,从而可得sinB的值.
解答 解:∵在直角△ABC中,∠C=90°,CD是斜边AB的中线,
∴AB=2CD.
∵CD=2,
∴AB=4.
∵AC=3,
∴sinB=$\frac{AC}{AB}=\frac{3}{4}$.
故选项A错误,选项B正确,选项C正确,选项D错误.
故选C.
点评 本题考查解直角三角形、直角三角线斜边上的中线等于斜边的一半,解题的关键是明确直角三角线的性质,找出所求问题需要的条件.

练习册系列答案
相关题目
 作图题:如图所示是毎一个小方格都是边长为1的正方形网格.
作图题:如图所示是毎一个小方格都是边长为1的正方形网格. 如图,BC为⊙O的直径,AD⊥BC,垂足为D,弧AB等于弧AF,BF和AD相交于E.
如图,BC为⊙O的直径,AD⊥BC,垂足为D,弧AB等于弧AF,BF和AD相交于E.