题目内容
2.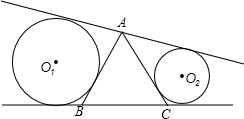 如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
如图,△ABC是等边三角形,边长为10,过A作不穿过三角形的直线l,以r1为半径的⊙O1与AB、l、BC相切,以r2为半径的⊙O2与AC、l、BC相切.求证:当l变化时,r1+r2始终为常数.
分析 先根据切线的性质得到EF的长,根据线段的和差求得EB+FC的值,然后根据三角函数的定义进而解决问题.
解答 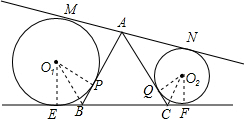 解:如图,设切点分别为M、N、E、F、P、Q,连接O1E,O1P,O1B,O2Q,O2C,O2F,
解:如图,设切点分别为M、N、E、F、P、Q,连接O1E,O1P,O1B,O2Q,O2C,O2F,
由切线定义,可得AM=AP,AN=AQ,EB=BP,FC=CQ,MN=EF,
∴MN+EF=30,MN=EF,
∴EF=15,
∴EB+FC=15-10=5,
∵∠EBP=120°,
∴∠EBO1=60°,
∴r1=$\sqrt{3}$EB,
同理r2=$\sqrt{3}$CF,
∴r1+r2=$\sqrt{3}$(EB+FC)=5$\sqrt{3}$.
∴当l变化时,r1+r2始终为常数.
点评 本题考查了切线的性质,等腰三角形的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
13.过n边形的一个顶点的所有对角线,将这个多边形分成8个三角形,则n=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
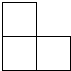 小红分别从正面、左面和上面观察由一些相同小立方块搭成的几何体时,发现几何体的形状图均为如图,则构成该几何体的小立方块的个数有( )
小红分别从正面、左面和上面观察由一些相同小立方块搭成的几何体时,发现几何体的形状图均为如图,则构成该几何体的小立方块的个数有( ) 如图,BC为⊙O的直径,AD⊥BC,垂足为D,弧AB等于弧AF,BF和AD相交于E.
如图,BC为⊙O的直径,AD⊥BC,垂足为D,弧AB等于弧AF,BF和AD相交于E.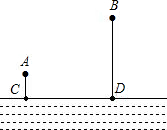 如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).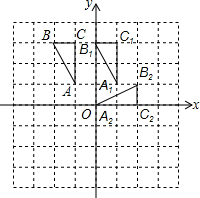 如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题:
如图,△ABC的三个顶点坐标分别为A(-1,1)、B(-2,3),C(-1,3),画图并完成下列问题: △ABC中,∠ACB=90°,点D是AC上一点,CE⊥BD于E,∠DAE=∠ABD,求证:
△ABC中,∠ACB=90°,点D是AC上一点,CE⊥BD于E,∠DAE=∠ABD,求证: