题目内容
17.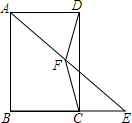 如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.
如图,在四边形ABCD中,AD∥BC,AD=BC,∠ABC=90°,点E在BC的延长线上,连接AE,点F为AE的中点.求证:DF=FC.
分析 连接BF,根据直角三角形性质求出AF=EF=BF,求出∠FBE=∠E,根据平行线性质得出∠DAF=∠E,求出∠DAF=∠FBE,根据SAS推出△ADF≌△BCF,根据全等三角形的性质得出即可.
解答 证明:连接BF,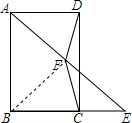
∵∠ABC=90°,
∴△ABE为直角三角形,
∵点F为AE的中点,
∴AF=EF=BF,
∴∠FBE=∠E,
又∵AD∥BC,
∴∠DAF=∠E,
∴∠DAF=∠FBE,
在△ADF和△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠DAF=∠CBF}\\{AF=AF}\end{array}\right.$,
∴△ADF≌△BCF,
∴DF=FC.
点评 此题主要考查了全等三角形的判定和性质定理,平行线的性质,直角三角形的性质的应用,关键是找出能使三角形全等的条件,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
7.下列算式正确的是( )
| A. | 32=6 | B. | (-$\frac{1}{4}$)÷(-4)=1 | C. | (-8)2=-16 | D. | -5-(-2)=-3 |
5.抛物线y=-3(x+2)2-4的开口方向和对称轴分别是( )
| A. | 向上,x=2 | B. | 向上,x=-2 | C. | 向下,x=2 | D. | 向下,x-=2 |
9.已知a2+2a=1,则代数式1-2a2-4a的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
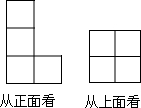 如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的.
如图所示,是由若干个完全相同的小正方体搭成的几何体的从正面和从上面看到的形状图,则这个几何体可能是由6或7或8个小正方体搭成的. 如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.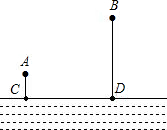 如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).
如图,A、B两个村子在河边CD的同侧,A、B两村到河边的距离分别为AC=1千米,BD=3千米,CD=3千米.现在河边CD建一座水厂,建成后的水厂,可以直接向A、B两村送水,也可以先将水送一村再转送至另一村.铺设水管费用为每千米2万元,试在河边CD选择水厂位置确定方案,使铺设水管费用最省.并求出铺设水管的总费用(精确到0.01万元).