题目内容
2．已知方程x2+3x-4=0，x1，x2为方程的两根，则x1+x2=-3．分析 直接根据根与系数的关系求解．
解答 解：根据题意得则x1+x2=-3．
故答案为-3．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
10．若字母A表示算式：$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$，则式子（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$）-（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）×（1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$）用含A的代数式表示为（ ）
| A． | （1+A）（A+$\frac{1}{6}$）-A（A+$\frac{1}{6}$） | B． | （1+A）（A+$\frac{1}{6}$）-A（A-$\frac{1}{6}$） | C． | （1+A）（A+$\frac{1}{6}$）-A（1+A） | D． | （1+A）（A+$\frac{1}{6}$）-A（A+$\frac{7}{6}$） |
17．一元二次方程2x2+5x+2=0的根的情况是（ ）
| A． | 有两个相等的实数根 | B． | 有两个不相等的实数根 | ||
| C． | 无实数根 | D． | 不能确定 |
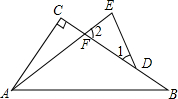如图，在△ABC中，∠C=90°，F、D是BC上两点，E是AF延长线上一点，∠B=∠1，∠E=∠2，BF=kDE．试探究AB、BC、DE之间的数量关系．（用含有k的代数式表示）