题目内容
求1+2+22+23+…+22013的值，可令S=1+2+22+23+…+22013，则2S=2+22+23+…+22014，因此2S-S=22014-1．仿照以上推理，计算出1+5+52+53+…+52014= ．
考点：有理数的乘方
专题：阅读型
分析：根据题目信息，设S=1+5+52+53+…+52014，表示出5S=5+52+53+…+52015，然后相减求出S即可．
解答：解：设S=1+5+52+53+…+52014，
则5S=5+52+53+…+52015，
5S-S=（5+52+53+…+52015）-（1+5+52+53+…+52014）=22015-1，
所以，S=
．
故答案为：
．
则5S=5+52+53+…+52015，
5S-S=（5+52+53+…+52015）-（1+5+52+53+…+52014）=22015-1，
所以，S=
| 22015-1 |
| 4 |
故答案为：
| 22015-1 |
| 4 |
点评：本题考查了有理数的乘方，读懂题目信息，理解等比数列的求和方法是解题的关键．
练习册系列答案
相关题目
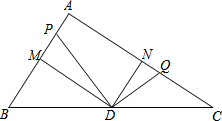如图，在Rt△ABC中，∠A=90°，AB=6，AC=8，点M、N分别为AB，AC边的中点，点D为BC边的中点，动点P从点A出发，沿射线AB方向移动，作∠PDQ=90°，点Q在AC上，设AP=x，CQ=y．
如图，在菱形ABCD中，AB：AC=m：n，点P为BC边上一点，以AP为对角线作菱形AFPM，满足∠ABC=∠AFP，连结BF，猜想BF与CP的数量关系，并证明你的结论．
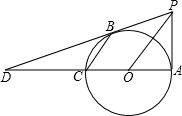如图，已知AC是⊙O的直径，PA⊥AC，连接OP，弦CB∥OP，直线PB交直线AC于点D．
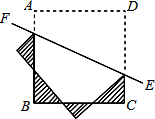如图，已知正方形ABCD的边长为2，将正方形ABCD沿直线EF折叠，则图中折成的4个阴影三角形的周长之和为
如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，则∠COD的度数是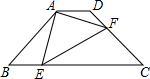
如图，在等腰梯形ABCD中，AD∥BC，BC=4AD=4