题目内容
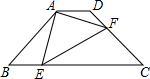 如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4
如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4| 2 |
考点:等腰梯形的性质
专题:
分析:由题意易证∠1=∠3,从而得出△ABE∽△ECF;由相似得出比例式,即可得出y是x的二次函数,求出y的最大值即可;当CF最大时,AF最小.
解答:解:设BE=x,CF=y
∵∠AEF=∠B=∠C=45°,
∴∠1+∠2=∠2+∠3=135°,
∴∠1=∠3,
∴△ABE∽△ECF;
AB=(4
-
)÷2×
=3,
由(1)得,
=
,即
=
,
∴y=
x(4
-x)=-
x2+
x(0<x<4
)
当x=2
即E为BC的中点时,ymax=
;
又∵当CF最大时,AF最小,
此时DF=DC-CF=3-
=
,
作FH⊥AD于H,则FH=DH=
,
∴AFmin=
=
=
.

故答案为:
.
∵∠AEF=∠B=∠C=45°,
∴∠1+∠2=∠2+∠3=135°,
∴∠1=∠3,
∴△ABE∽△ECF;
AB=(4
| 2 |
| 2 |
| 2 |
由(1)得,
| BE |
| CF |
| AB |
| CE |
| x |
| y |
| 3 | ||
4
|
∴y=
| 1 |
| 3 |
| 2 |
| 1 |
| 3 |
4
| ||
| 3 |
| 2 |
当x=2
| 2 |
| 8 |
| 3 |
又∵当CF最大时,AF最小,
此时DF=DC-CF=3-
| 8 |
| 3 |
| 1 |
| 3 |
作FH⊥AD于H,则FH=DH=
| ||
| 6 |
∴AFmin=
| AH2+FH2 |
| 10 |
| 6 |
| 5 |
| 3 |

故答案为:
| 5 |
| 3 |
点评:本题考查了相似三角形的判定和性质、二次函数的最值问题以及等腰梯形的性质,是一道综合题,难度较大.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,该几何体的左视图是( )
如图,该几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
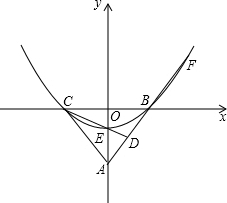 如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC= 如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=
如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE= 如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为
如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为 如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.
如图,在△ABC中,D是AB边上一点,⊙O过D、B、C三点,∠DOC=2∠ACD=90°.