题目内容
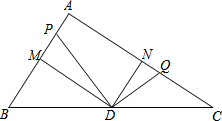 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y.(1)证明:△PDM∽△QDN;
(2)求y与x的函数关系式,并求x的取值范围;
(3)问x为何值时,△CDQ是等腰三角形?
考点:相似形综合题
专题:
分析:(1)根据已知和中位线的性质得出∠DMP=∠DNQ=∠MDN=90°,再根据∠PDQ=90°,得出∠PDM=∠QDN,最后根据AA得出△PDM∽△QDN;
(2)根据(1)得出
=
=
,求出QN=
PM,分别进行讨论若点P在AM上,则点Q在CN上和若点P在MB上,则点Q在NA上,用x表示出PM和QN,求出y与x的函数关系式,当点Q与点A重合时,求出CQ=8,从而得出x的取值范围;
(3)根据点D为Rt△ABC斜边BC的中点,得出DA=DC=5,由(2)知,点Q与点A重合,△CDQ是等腰三角形,求出x的值;当CQ=CD=5,QN=CQ-CN=1,求出x的值;若CQ=DQ,过点Q作QE⊥DC,得出CH=
,cos∠C=
,在Rt△ABC中,求出cos=∠C的值,从而求出x的值即可.
(2)根据(1)得出
| PM |
| QN |
| DM |
| DN |
| 4 |
| 3 |
| 3 |
| 4 |
(3)根据点D为Rt△ABC斜边BC的中点,得出DA=DC=5,由(2)知,点Q与点A重合,△CDQ是等腰三角形,求出x的值;当CQ=CD=5,QN=CQ-CN=1,求出x的值;若CQ=DQ,过点Q作QE⊥DC,得出CH=
| 5 |
| 2 |
| CH |
| CQ |
解答:解:(1)∵点M、N分别为AB,AC边的中点,点D为BC边的中点,
∴DM,DN是中位线,
∵∠A=90°,
∴∠DMP=∠DNQ=∠MDN=90°,
∵∠PDQ=90°,
∴∠PDM=90°-∠PDN,∠QDN=90-∠PDN,
∴∠PDM=∠QDN,
∴△PDM∽△QDN;
(2)∵AB=6,AC=8,
∴DM=4,DN=3,
∵△PDM∽△QDN,
∴
=
=
,
∴QN=
PM,
若点P在AM上,则点Q在CN上,PM=3-x,QN=
(3-x),y=CQ=CN-QN=4-
(3-x)=
+
x,
若点P在MB上,则点Q在NA上,PM=x-3,QN=
(x-3),y=CQ=CN+QN=4+
(x-3)=
+
x,
∴所求的函数关系式是y=
x+
,
当点Q与点A重合时,即CQ=8,此时,
x+
=8,
解得:x=
,
∴x的取值范围是0≤x≤
;
(3)∵点D为Rt△ABC斜边BC的中点,
∴DA=DC=5,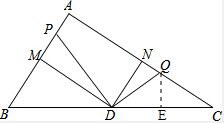
由(2)可知,点Q与点A重合,△CDQ是等腰三角形,此时,x=
,
若CQ=CD=5,QN=CQ-CN=1,此时PM=
QN=
,
x=AP=3+
=
,
若CQ=DQ,过点Q作QE⊥DC,则CE=
,cos∠C=
,
在Rt△ABC中,cos∠C=
=
,
∴
=
,CQ=
CE=
,
∴
x+
=
,
解得:x=
.
综上所述:当x=
或
或
时,△CDQ是等腰三角形.
∴DM,DN是中位线,
∵∠A=90°,
∴∠DMP=∠DNQ=∠MDN=90°,
∵∠PDQ=90°,
∴∠PDM=90°-∠PDN,∠QDN=90-∠PDN,
∴∠PDM=∠QDN,
∴△PDM∽△QDN;
(2)∵AB=6,AC=8,
∴DM=4,DN=3,
∵△PDM∽△QDN,
∴
| PM |
| QN |
| DM |
| DN |
| 4 |
| 3 |
∴QN=
| 3 |
| 4 |
若点P在AM上,则点Q在CN上,PM=3-x,QN=
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
若点P在MB上,则点Q在NA上,PM=x-3,QN=
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
∴所求的函数关系式是y=
| 3 |
| 4 |
| 7 |
| 4 |
当点Q与点A重合时,即CQ=8,此时,
| 3 |
| 4 |
| 7 |
| 4 |
解得:x=
| 25 |
| 3 |
∴x的取值范围是0≤x≤
| 25 |
| 3 |
(3)∵点D为Rt△ABC斜边BC的中点,
∴DA=DC=5,

由(2)可知,点Q与点A重合,△CDQ是等腰三角形,此时,x=
| 25 |
| 3 |
若CQ=CD=5,QN=CQ-CN=1,此时PM=
| 4 |
| 3 |
| 4 |
| 3 |
x=AP=3+
| 4 |
| 3 |
| 13 |
| 3 |
若CQ=DQ,过点Q作QE⊥DC,则CE=
| 5 |
| 2 |
| CE |
| CQ |
在Rt△ABC中,cos∠C=
| AC |
| BC |
| 4 |
| 5 |
∴
| CE |
| CQ |
| 4 |
| 5 |
| 5 |
| 4 |
| 25 |
| 8 |
∴
| 3 |
| 4 |
| 7 |
| 4 |
| 25 |
| 8 |
解得:x=
| 11 |
| 6 |
综上所述:当x=
| 25 |
| 3 |
| 13 |
| 3 |
| 11 |
| 6 |
点评:此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、中位线的性质、等腰三角形的性质以及特殊角的三角函数值,关键是利用数形结合思想进行解答.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
 如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=
如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA= 如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数.
如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数. 如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=