题目内容
 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是考点:多边形内角与外角,三角形内角和定理
专题:
分析:首先根据四边形内角和可得∠ADC+∠DCB=360°-200°=160°,再根据角平分线的性质可得∠ODC+∠OCD=
×160°=80°,再进一步利用三角形内角和定理可得答案.
| 1 |
| 2 |
解答:解:∵四边形ABCD中,∠A+∠B=200°,
∴∠ADC+∠DCB=360°-200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=
∠ADC,∠OCD=
∠BCD,
∴∠ODC+∠OCD=
×160°=80°,
∴∠COD=180°-80°=100°,
故答案为:100°.
∴∠ADC+∠DCB=360°-200°=160°,
∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ODC+∠OCD=
| 1 |
| 2 |
∴∠COD=180°-80°=100°,
故答案为:100°.
点评:此题主要考查了多边形内角和定理,关键是掌握多边形内角和定理:(n-2).180 (n≥3)且n为整数).

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 如图,该几何体的左视图是( )
如图,该几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数.
如图,在△ABC中AB=AC,∠A=56°,BD⊥AC于D,求∠CBD的度数.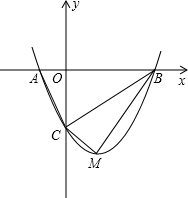 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交与A、B两点,与y轴交与C点.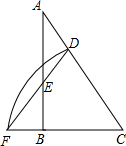 如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC=
如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC= 如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=
如图,AD是△ABC的角平分线,DE∥AB交AC于点E,AB=8,AC=6,则DE=