题目内容
10.一个直棱柱,主视图是边长为2$\sqrt{3}$的正方形、俯视图是边长为2$\sqrt{3}$的正三角形,则左视图的面积为( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 首先根据题意画出俯视图和主视图,然后计算出正三角形的高,再根据主视图是边长为2$\sqrt{3}$的正方形计算出左视图的面积即可.
解答  解:过A作AD⊥BC,
解:过A作AD⊥BC,
∵俯视图是边长为2$\sqrt{3}$的正三角形,
∴BC=2$\sqrt{3}$,∠B=60°,
∴AD=ABsin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∵主视图是边长为2$\sqrt{3}$的正方形,
∴左视图的面积为3×$2\sqrt{3}$=6$\sqrt{3}$,
故选:C.
点评 此题主要考查了简单几何体的三视图,关键是掌握主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
19.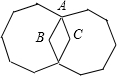 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )
 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )| A. | 60° | B. | 45° | C. | 30° | D. | 72° |

 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图和左视图的面积之和是5.
如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图和左视图的面积之和是5.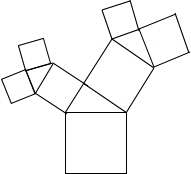 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.