题目内容
20.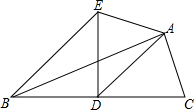 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 根据折叠的性质判定△EDB是等腰直角三角形,然后再求BE.
解答 解:根据折叠的性质知,CD=ED,∠CDA=∠ADE=45°,
∴∠CDE=∠BDE=90°,
∵BD=CD,BC=6,
∴BD=ED=3,
即△EDB是等腰直角三角形,
∴BE=$\sqrt{2}$BD=$\sqrt{2}$×3=3$\sqrt{2}$,
故选D.
点评 本题考查了翻折变换,还考查的知识点有两个:1、折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;2、等腰直角三角形的性质求解.

练习册系列答案
相关题目
11. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
8.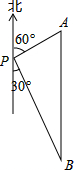 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )| A. | 60海里 | B. | 45海里 | C. | 20$\sqrt{3}$海里 | D. | 30$\sqrt{3}$海里 |
15.面积为2的正方形的边长在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
5.下列运算正确的是( )
| A. | 8a-a=8 | B. | (-a)4=a4 | C. | a3•a2=a6 | D. | (a-b)2=a2-b2 |
9.下列计算正确的是( )
| A. | x2+3x2=4x4 | B. | x2y•2x3=2x4y | C. | (6x3y2)÷(3x)=2x2 | D. | (-3x)2=9x2 |
10.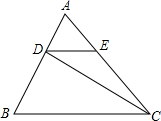 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )| A. | 1:5 | B. | 1:12 | C. | 1:8 | D. | 1:9 |
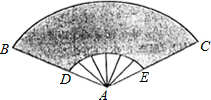 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π).
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π). 如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.
如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.