题目内容
10.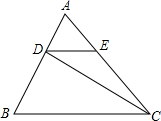 如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )
如图,在△ABC中,DE∥BC,且S△ADE:S△CDE=1:3,则S△ADE:S△DBC等于( )| A. | 1:5 | B. | 1:12 | C. | 1:8 | D. | 1:9 |
分析 根据等高的三角形的面积比等于对应的边之比得出AE:EC=1:4,根据平行线分线段成比例定理推出$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{1}{3}$,然后根据相似三角形的性质即可得到结论.
解答 解:∵△ADE的边AE上的高和△CDE的边CE上的高相等,
∵S△ADE:S△CDE=1:3,
∴$\frac{AE}{CE}$=$\frac{1}{3}$,
∵DE∥BC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$=$\frac{1}{3}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{1}{16}$,
设S△ADE=k,则S△CDE=3k,S△ABC=16k,
∴S△BCD=S△ABC-S△ADE-S△CDE=12k,
∴S△ADE:S△DBC=1:12.
故选B.
点评 本题考查了平行线分线段成比例定理和三角形的面积公式的应用,关键是求出AE:EC的比和得出AD:DB=AE:EC.

练习册系列答案
相关题目
20.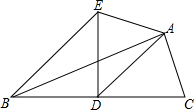 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
18.为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,这四组数据的众数是( )
| A. | 52和54 | B. | 52 | C. | 53 | D. | 54 |
15.若|a+2|=a+2,则a的取值范围是( )
| A. | a≥-2 | B. | a≤-2 | C. | a<-2 | D. | a>-2 |
2. 如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )
如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )
 如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )
如图,△ABC中,AE是∠BAC的角平分线,AD是BC边上的高线,且∠B=50°,∠C=60°,则∠EAD的度数( )| A. | 35° | B. | 5° | C. | 15° | D. | 25° |
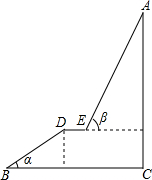 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).