题目内容
11. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据扇形的圆心角的度数和直径BC的长确定扇形的半径,然后确定扇形的弧长,根据圆锥的底面周长等于扇形的弧长列式求解即可.
解答  解:如图,连接AO,∠BAC=120°,
解:如图,连接AO,∠BAC=120°,
∵BC=2$\sqrt{3}$,∠OAC=60°,
∴OC=$\sqrt{3}$,
∴AC=2,
设圆锥的底面半径为r,则2πr=$\frac{120π×2}{180}$=$\frac{4}{3}$π,
解得:r=$\frac{2}{3}$,
故选B.
点评 本题考查了圆锥的计算,解题的关键是能够了解圆锥的底面周长等于展开扇形的弧长,难度不大.

练习册系列答案
相关题目
1.下列各数中,不是负数的是( )
| A. | -2 | B. | 3 | C. | -$\frac{5}{8}$ | D. | -0.10 |
3.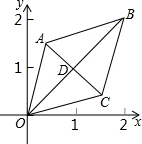 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )| A. | (1,-1) | B. | (-1,-1) | C. | ($\sqrt{2}$,0) | D. | (0,-$\sqrt{2}$) |
20.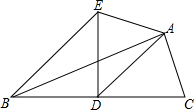 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |

 如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=5.
如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE=5.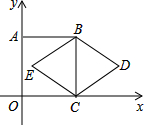 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是(2+$\sqrt{3}$,1).
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是(2+$\sqrt{3}$,1).