题目内容
8．
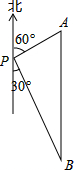如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为（ ）| A． | 60海里 | B． | 45海里 | C． | 20$\sqrt{3}$海里 | D． | 30$\sqrt{3}$海里 |
分析 根据题意得出：∠B=30°，AP=30海里，∠APB=90°，再利用勾股定理得出BP的长，求出答案．
解答 解：由题意可得：∠B=30°，AP=30海里，∠APB=90°，
故AB=2AP=60（海里），
则此时轮船所在位置B处与灯塔P之间的距离为：BP=$\sqrt{A{B}^{2}-A{P}^{2}}$=30$\sqrt{3}$（海里）
故选：D．
点评 此题主要考查了勾股定理的应用以及方向角，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，E是斜边AB的中点，若AB=10，则CE=5．
3．
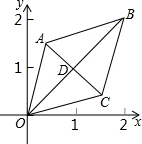如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（ ）
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（ ）| A． | （1，-1） | B． | （-1，-1） | C． | （$\sqrt{2}$，0） | D． | （0，-$\sqrt{2}$） |
13．某班7名女生的体重（单位：kg）分别是35、37、38、40、42、42、74，这组数据的众数是（ ）
| A． | 74 | B． | 44 | C． | 42 | D． | 40 |
20．
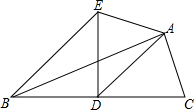如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（ ）
如图，AD是△ABC的中线，∠ADC=45°，把△ADC沿着直线AD对折，点C落在点E的位置．如果BC=6，那么线段BE的长度为（ ）| A． | 6 | B． | 6$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 3$\sqrt{2}$ |
17．要使式子$\frac{\sqrt{x-1}}{2}$有意义，则x的取值范围是（ ）
| A． | x＞1 | B． | x＞-1 | C． | x≥1 | D． | x≥-1 |