题目内容
5.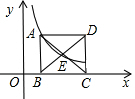 已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
分析 把已知点的坐标代入函数解析式即可求出k的值,把k的值代入得到函数的解析式,然后根据正方形的性质设出A的坐标,根据正方形的性质表示出点E的坐标,代入解析式求得未知数的值,即可得点E的坐标.
解答 解:把(1,3)代入到y=$\frac{k}{x}$得:k=3,
故函数解析式为y=$\frac{3}{x}$,
设A(a,$\frac{3}{a}$)(a>0),根据图象和题意可知,点E(a+$\frac{3}{2a}$,$\frac{3}{2a}$),
因为y=$\frac{3}{x}$的图象经过E,
所以将E代入到函数解析式中得:$\frac{3}{2a}$(a+$\frac{3}{2a}$)=3,
即a2=$\frac{3}{2}$,
求得:a=$\frac{\sqrt{6}}{2}$或a=-$\frac{\sqrt{6}}{2}$(不合题意,舍去),
∴a=$\frac{\sqrt{6}}{2}$,
∴a+$\frac{3}{2a}$=$\sqrt{6}$,$\frac{3}{2a}$=$\frac{\sqrt{6}}{2}$
则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$),
故答案为:($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
点评 本题主要考查反比例函数图象上点的坐标特征和正方形的性质,熟练掌握正方形的性质表示出点E的坐标是解题的关键.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | -a(a-b)=-a2-ab | B. | (2ab)2÷a2b=4ab | C. | 2ab×3a=6a2b | D. | (a-1)(1-a)=a2 |
20.下列各数是无理数的是( )
| A. | 0 | B. | 2 | C. | -3 | D. | $\sqrt{2}$ |
17.下列图形中,是中心对称但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.若a>b,则下列不等式中错误的是( )
| A. | a-1>b-1 | B. | a+1>b+1 | C. | 2a>2b | D. | -3a>-3b |
15.下列运算中不正确的是( )
| A. | a3+a2=a5 | B. | a3•a2=a5 | C. | a3÷a2=a | D. | (a3)2=a6 |