题目内容
10.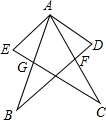 如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
分析 先由SAS证明△BAF≌△CAG,得出对应角相等∠B=∠C,再由AAS证明△AEC≌△ADB,得出对应边相等即可.
解答 已知:在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,AB=AC,AF=AG,AD⊥BD,AE⊥CE;
求证:AD=AE;
证明:在△BAF与△CAG中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAF=∠CAG}\\{AF=AG}\end{array}\right.$,
∴△BAF≌△CAG(SAS),
∴∠B=∠C,
∵AD⊥BD,AE⊥CE,
∴∠E=∠D=90°,
在△AEC与△ADB中,$\left\{\begin{array}{l}{∠E=∠D}\\{AB=AC}\\{∠B=∠C}\end{array}\right.$,
∴△AEC≌△ADB(AAS),
∴AD=AE.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
20.下列图形既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
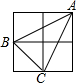 如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.
如图,2×2的方格中,小正方形的边长是1,点A、B、C都在格点上,则△ABC中AB边上的高长为$\frac{3\sqrt{5}}{5}$.
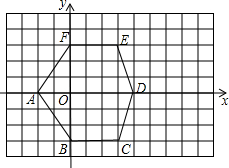 观察图,并回答一下问题:
观察图,并回答一下问题: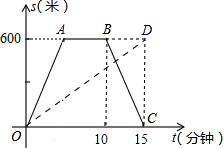 甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )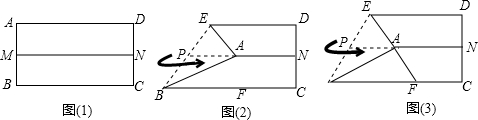
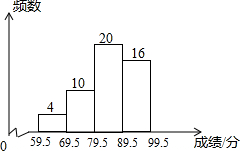 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题: