题目内容
已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,则∠DOE= .
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,则∠DOE= .
(3)如图③,当射线OC在∠AOB外绕O点旋转时,在备用图中画出图形,判断∠DOE的大小是否发生变化?若变化,说明理由;若不变,求∠DOE的度数.
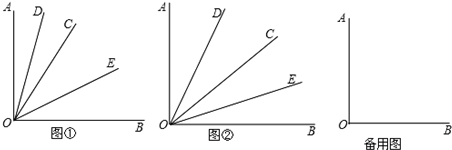
(1)如图①,当∠BOC=70°时,则∠DOE=
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,则∠DOE=
(3)如图③,当射线OC在∠AOB外绕O点旋转时,在备用图中画出图形,判断∠DOE的大小是否发生变化?若变化,说明理由;若不变,求∠DOE的度数.

考点:角的计算,角平分线的定义
专题:
分析:(1)根据∠AOB是一个直角,OD,OE,分别平分∠AOC和∠BOC,以及∠BOC=70°,即可得出∠DOC与∠COE的度数;
(2)根据(1)中结论以及∠BOC=α,分别表示出∠DOE=∠DOC+∠COE=
∠COB+
∠AOC求出即可;
(3)正确作出图形,根据角平分线的性质判断大小变化.
(2)根据(1)中结论以及∠BOC=α,分别表示出∠DOE=∠DOC+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)正确作出图形,根据角平分线的性质判断大小变化.
解答:解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=
∠COB=35°,∠COD=
∠AOC=10°,
∴∠DOE=45°;
故答案是:45°;
(2)∵当∠BOC=α时,
理由:∠DOE=∠DOC+∠COE=
∠COB+
∠AOC
=
(∠COB+∠AOC)
=
∠AOB
=45°;
故答案是:45°;
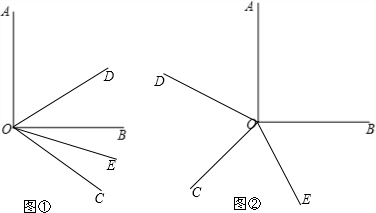
(3)∠DOE的大小发生变化,∠DOE=45°或135°.
如图①,则∠DOE=45°;如图②,则∠DOE=135°.
∴∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=45°;
故答案是:45°;
(2)∵当∠BOC=α时,
理由:∠DOE=∠DOC+∠COE=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°;
故答案是:45°;
(3)∠DOE的大小发生变化,∠DOE=45°或135°.
如图①,则∠DOE=45°;如图②,则∠DOE=135°.

点评:此题主要考查了角平分线的性质以及角的有关计算,正确作图,熟记角的特点与角平分线的定义是解决此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知A样本的数据如下:72,73,76,76,77,78,78,78.B样本的数据恰好是A样本数据每个都加2,则A、B两个样本具有相同的( )
| A、平均数 | B、众数 |
| C、中位数 | D、方差 |
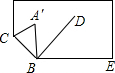 如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )
如图所示,将一长方形纸的一角斜折过去,使顶点A落在A′处,BC为折痕,如果BD为∠A′BE的平分线,则∠CBD=( )| A、90° | B、80° |
| C、100° | D、70° |
 二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
二次函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号实数根 |
| C、有两个相等的实数根 |
| D、无实数根 |
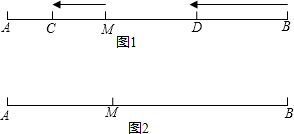 如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示. 已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.
已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE. 如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据: