题目内容
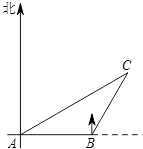 如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:
如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点C作CD⊥AB,交AB延长线于点D,根据题意求出CD的长,再和岛C的半径12海里比较大小即可得到问题答案.
解答: 解:过点C作CD⊥AB,交AB延长线于点D.由题意可知,
解:过点C作CD⊥AB,交AB延长线于点D.由题意可知,
在△ABC中,∠CAB=30°,∠ABC=90°+30°=120°,
∴∠ACB=30°,BC=AB=20.
在Rt△CBD中,∠CBD=60°,
∴CD=CB•sin∠CBD=10
(海里).
∵10
>12,
∴这艘渔船继续向东航行追赶鱼群不会进入危险区.
 解:过点C作CD⊥AB,交AB延长线于点D.由题意可知,
解:过点C作CD⊥AB,交AB延长线于点D.由题意可知,在△ABC中,∠CAB=30°,∠ABC=90°+30°=120°,
∴∠ACB=30°,BC=AB=20.
在Rt△CBD中,∠CBD=60°,
∴CD=CB•sin∠CBD=10
| 3 |
∵10
| 3 |
∴这艘渔船继续向东航行追赶鱼群不会进入危险区.
点评:此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
在四边形ABCD中,已知AD∥BC,若再从下列条件:①∠A+∠C=180°;②AB=CD;③∠A+∠B=180°;④∠A+∠D=180°中任意选取一个来判定四边形ABCD是平行四边形,则能断定四边形ABCD是平行四边形的选法共有( )
| A、1种 | B、2种 | C、3种 | D、4种 |
 如图,A,B,C都是⊙O上的点,若∠ABC=110°,则∠AOC的度数为( )
如图,A,B,C都是⊙O上的点,若∠ABC=110°,则∠AOC的度数为( )| A、70° | B、110° |
| C、135° | D、140° |
 李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米.要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米.要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )A、y=-
| ||
| B、y=-2x+24 | ||
| C、y=2x-24 | ||
D、y=
|
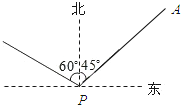 如图,某港口P位于东西方向的海岸线上,小岛A在港口P的北偏东45°方向上,距离港口80海里,“远航”号从A出发,沿AP方向以10海里/小时的速度驶向港口,“海天”号从港口P出发,沿北偏西60°方向,以20海里/小时的速度驶离港口,现两船同时出发,试问出发几小时,“海天”号在“远航”号的正西方向?(
如图,某港口P位于东西方向的海岸线上,小岛A在港口P的北偏东45°方向上,距离港口80海里,“远航”号从A出发,沿AP方向以10海里/小时的速度驶向港口,“海天”号从港口P出发,沿北偏西60°方向,以20海里/小时的速度驶离港口,现两船同时出发,试问出发几小时,“海天”号在“远航”号的正西方向?(
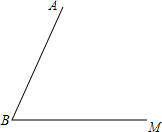 已知:如图,线段AB和射线BM交于点B.
已知:如图,线段AB和射线BM交于点B.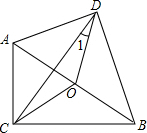 如图,在四边形ABCD中,∠ACB=∠ADB=90°,O是AB的中点,若∠CAB=60°,∠DBA=40°,则∠1=
如图,在四边形ABCD中,∠ACB=∠ADB=90°,O是AB的中点,若∠CAB=60°,∠DBA=40°,则∠1= 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),