题目内容
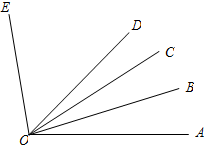 已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.
已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.(1)求∠COD的度数;
(2)若以O为观察中心,OA为正东方向,射线OD的方向角是
(3)若∠AOE的两边OA、OE分别以每秒5°、每秒3°的速度,同时绕点O逆时针方向旋转,当OA回到原处时,OA、OE停止运动,则经过几秒,∠AOE=42°.
考点:角的计算,方向角,角平分线的定义
专题:
分析:(1)根据图示得到∠EOB=80°;然后由角平分线的定义来求∠COD的度数;
(2)根据方向角的表示方法,可得答案;
(3)设经过x秒,∠AOE=42°则依据题意列出方程并解答即可.
(2)根据方向角的表示方法,可得答案;
(3)设经过x秒,∠AOE=42°则依据题意列出方程并解答即可.
解答: 解:(1)∵∠AOB=20°,∠AOE=100°,
解:(1)∵∠AOB=20°,∠AOE=100°,
∴∠EOB=∠AOE-∠AOB=80°.
又∵OB平分∠AOC,OD平分∠AOE,
∴∠AOC=2∠AOB=40°,∠AOD=
∠AOE=50°,
∴∠COD=∠AOD-∠AOC=50°-40°=10°;
(2)由(1)知,∠AOD=50°,
射线OD在东偏北50°,即射线OD在北偏东40°;
故答案是:北偏东40°;
(3)设经过x秒,∠AOE=42°则
3x-5x+100°=42°,
解得 x=29.
即经过29秒,∠AOE=42°.
 解:(1)∵∠AOB=20°,∠AOE=100°,
解:(1)∵∠AOB=20°,∠AOE=100°,∴∠EOB=∠AOE-∠AOB=80°.
又∵OB平分∠AOC,OD平分∠AOE,
∴∠AOC=2∠AOB=40°,∠AOD=
| 1 |
| 2 |
∴∠COD=∠AOD-∠AOC=50°-40°=10°;
(2)由(1)知,∠AOD=50°,
射线OD在东偏北50°,即射线OD在北偏东40°;
故答案是:北偏东40°;
(3)设经过x秒,∠AOE=42°则
3x-5x+100°=42°,
解得 x=29.
即经过29秒,∠AOE=42°.
点评:本题考查了方向角,利用了角平分线的性质,角的和差,方向角的表示方法.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
关于单项式(-5)2x3y,下列说法正确的是( )
| A、次数是6 | B、系数是-5 |
| C、次数是3 | D、系数是25 |
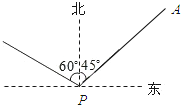 如图,某港口P位于东西方向的海岸线上,小岛A在港口P的北偏东45°方向上,距离港口80海里,“远航”号从A出发,沿AP方向以10海里/小时的速度驶向港口,“海天”号从港口P出发,沿北偏西60°方向,以20海里/小时的速度驶离港口,现两船同时出发,试问出发几小时,“海天”号在“远航”号的正西方向?(
如图,某港口P位于东西方向的海岸线上,小岛A在港口P的北偏东45°方向上,距离港口80海里,“远航”号从A出发,沿AP方向以10海里/小时的速度驶向港口,“海天”号从港口P出发,沿北偏西60°方向,以20海里/小时的速度驶离港口,现两船同时出发,试问出发几小时,“海天”号在“远航”号的正西方向?( 如图,OC平分∠AOD,且∠2:∠3:∠4=1:2:4,求∠1的度数.
如图,OC平分∠AOD,且∠2:∠3:∠4=1:2:4,求∠1的度数.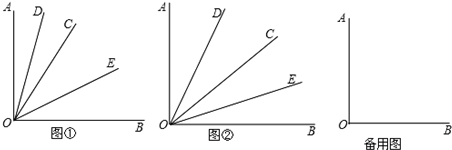
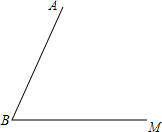 已知:如图,线段AB和射线BM交于点B.
已知:如图,线段AB和射线BM交于点B.