题目内容
14. 已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积?
已知某开发区有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求这块空地的面积?
分析 仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
解答  解:连接BD,如图所示:
解:连接BD,如图所示:
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD•BC=36m2;
答:这块空地的面积为36m2.
点评 本题考查了勾股定理以及逆定理;通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列说法中:①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;②八边形的内角和度数为1080°;③2、3、4、3这组数据的方差为0.5;④分式方程$\frac{1}{x}$=$\frac{3x-1}{x}$的解为x=$\frac{2}{3}$;⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2$\sqrt{3}$.正确的序号有( )
| A. | ①②③⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ②③④⑤ |
19.下列大学的校徽图案是轴对称图形的是( )
| A. |  清华大学 | B. |  北京大学 | C. |  北京人民大学 | D. |  浙江大学 |
6.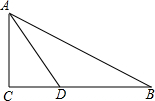 如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
 如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )| A. | 5 | B. | 10 | C. | 15 | D. | 无法确定 |
3.以下图形中不是轴对称图形的是( )
| A. | 正方形 | B. | 等边三角形 | C. | 矩形 | D. | 平行四边形 |
 如图,ABCD是一块平行四边形田地,P为水井,现要把这块田地平均分给甲,乙两户,为了方便用水,要求两户分到的田地都与水井相邻,试在图中画出方案,并给予必要的解释,以说明方案是正确合理的.
如图,ABCD是一块平行四边形田地,P为水井,现要把这块田地平均分给甲,乙两户,为了方便用水,要求两户分到的田地都与水井相邻,试在图中画出方案,并给予必要的解释,以说明方案是正确合理的.