题目内容
17.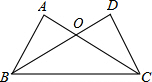 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.(1)求证:△ABC≌△DCB;
(2)若点O为AC的中点,S△ODC=1,直接写出S△OBC的值.
分析 (1)由已知条件,结合公共边可以利用SSS判定△ABC≌△DCB;
(2)由△ABC≌△DCB可知∠ACB=∠DBC,则OB=OC,又AC=BD,点O为AC的中点,则点O为BD的中点,于是S△OBC=S△ODC.
解答 解:(1)在△ABC和△DCB中
$\left\{\begin{array}{l}{AB=DC}\\{BC=CB}\\{AC=BD}\end{array}\right.$,
∴△ABC≌△DCB(SSS).
(2)∵△ABC≌△DCB,
∴∠DBC=∠ACB,
∴OB=OC,
∵AC=BD,点O为AC的中点,
∴点O为BD的中点,
∴S△OBC=S△ODC=1.
点评 此题考查了全等三角形的判定和等腰三角形的判定以及等底同高的三角形等积的性质,要牢固掌握并灵活运用,证明三角形全等是解答本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
5.一个多边形的内角和的度数是外角和的2倍,则这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 六边形 | D. | 八边形 |
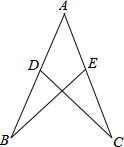 如图,点D,E分别在AB,AC上,AB=AC,BD=CE,求证:BE=CD.
如图,点D,E分别在AB,AC上,AB=AC,BD=CE,求证:BE=CD.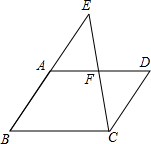 如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD.
如图,在?ABCD中,点E在BA的延长线上,连结CE交AD于点F,且F是AD的中点,求证:AE=CD. 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:
如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证: