题目内容
7.计算:$\sqrt{6}×\sqrt{\frac{1}{2}}-\sqrt{27}$=-2$\sqrt{3}$.分析 先根据二次根式的乘法运算,然后化简后合并即可.
解答 解:原式=$\sqrt{6×\frac{1}{2}}$-3$\sqrt{3}$
=$\sqrt{3}$-3$\sqrt{3}$
=-2$\sqrt{3}$.
故答案为-2$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
15.下列运算中,计算结果正确的是( )
| A. | 3x-2x=1 | B. | x•x=x2 | C. | 2x+2x=2x2 | D. | (-a3)2=a5 |
2.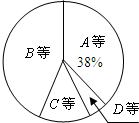 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
(1)试直接写出x、y的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
 某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.
某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成下面的频数分布表和扇形统计图.| 等第 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | 0.24 | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | 1 | y | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
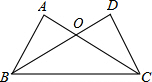 如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.
如图,在△ABC和△DCB中,AC与BD相交于点O,AB=DC,AC=BD.