题目内容
17.(1)计算:($\sqrt{6}$)2-$\sqrt{(-5)^{2}}$+$\root{3}{-27}$(2)若$\frac{1}{2}$(2x-1)3=-4,求x的值.
分析 (1)首先计算乘方和开方,然后从左向右依次计算,求出算式的值是多少即可.
(2)根据立方根的含义和求法,求出x的值是多少即可.
解答 解:(1)${(\sqrt{6})}^{2}$-$\sqrt{(-5)^{2}}$+$\root{3}{-27}$
=6-5-3
=-2
(2)∵$\frac{1}{2}$(2x-1)3=-4,
∴(2x-1)3=-8,
∴2x-1=-2,
解得x=-$\frac{1}{2}$.
点评 此题主要考查了实数的运算,以及立方根的求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
相关题目
7.下列利用乘法公式运算中错误的是( )
| A. | (-a+b)(-a-b)=a2-b2 | B. | (-a-b)2=a2+b2+2ab | C. | (-a+b)2=a2+b2-2ab | D. | (-a-b)(a+b)=a2-b2 |
5.在以下现象中,属于平移的是( )
①在挡秋千的小朋友
②电梯上升过程
③宇宙中行星的运动
④生产过程中传送带上的电视机的移动过程.
①在挡秋千的小朋友
②电梯上升过程
③宇宙中行星的运动
④生产过程中传送带上的电视机的移动过程.
| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
2.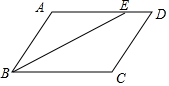 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
 如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )
如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于E,∠AEB=25°,则∠A的大小为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
9.下列运算错误的是( )
| A. | x3x2=x5 | B. | -x2-x2=-2x2 | C. | (-2x)2=-4x2 | D. | (-2x)(-3x2)=6x3 |
 如图,∠1=∠2,D为BC的中点,求证:AB=AC.
如图,∠1=∠2,D为BC的中点,求证:AB=AC.